Pí (číslo)

K označení konstanty se používá malé π

Ludolfovo číslo, značené π (čteme pí) je matematická konstanta, která udává poměr obvodu jakéhokoli kruhu v eukleidovské rovině k jeho průměru; také je to hodnota poměru obsahu kruhu ke čtverci jeho poloměru. Její hodnota v desítkové soustavě je přibližně 3,141592653589 (lze použít praktické racionální aproximace 22/7 pro orientační výpočty vyžadující přesnost hodnoty pouze na setiny resp. 355/113 pro přesnost pouze na miliontiny). Mnoho matematických, vědeckých a inženýrských rovnic obsahuje pí, což z něj dělá jednu z nejdůležitějších matematických konstant.

π je iracionální číslo, což znamená, že nemůže být vyjádřeno zlomkem m/n, kde m je celé číslo a n je přirozené číslo. To také znamená, že jej nelze vyjádřit konečným způsobem v desítkové soustavě, a to ani pomocí periody. Navíc je π dokonce transcendentní číslo, z čehož mimo jiné vyplývá, že ho nelze vyjádřit konečně dlouhou řadou algebraických operací s celými čísly; důkaz tohoto tvrzení byl výsledkem německé matematiky 19. století. V dějinách matematiky se objevují snahy o čím dál přesnější vyjádření π a pochopení jeho povahy; fascinace tímto číslem se promítla i mimo sféru matematiky.

Nejspíše pro jednoduchost své definice se π promítlo do populární kultury více než téměř všechny jiné matematické konstrukty. Stalo se nejspíše nejběžnějším společným tématem mezi matematiky a nematematiky. Zprávy o nejnovějším, nejpřesnějším odhadu π se běžně objevují v tisku. V červnu 2024 např. Jordan Ranous ze StorageReview Lab v americkém Cincinnati publikoval rekord v nejpřesnějším odhadu π v desítkové soustavě, který má 202 bilionů číslic; výpočet trval 104 dní.

Konstantě se říká Ludolfovo číslo po Ludolphovi van Ceulenovi. Spíše historické (ale např. v angličtině používané) je označení Archimédova konstanta po Archimédovi ze Syrakus.

Základy

Malé π označující konstantu. Mozaika před budovou matematiky na Technické univerzitě v Berlíně

Písmeno π

Řecké písmeno π (pí) pro označení tohoto čísla použil poprvé velšský matematik William Jones v roce 1706 jako zkratku řeckého slova pro obvod, řecky: περίμετρος (perimetros), či spíše περιφέρεια (periphéreia) okraj, vnější hranice. Toto označení zpopularizoval Leonhard Euler v roce 1737.

Geometrická definice

V eukleidovské geometrii je π definováno jako poměr délky o kružnice k jejímu průměru d:

Poměr o/d je konstantní, nezávisí na obvodu kružnice. Pokud má například kružnice dvakrát větší průměr než druhá, má také dvakrát větší obvod.

π může být také definováno jako poměr obsahu S kruhu ke čtverci poloměru r kružnice:

Tyto definice závisí na důsledcích eukleidovské geometrie, třeba že všechny kružnice jsou si podobné a že pravé strany těchto dvou rovnic jsou si rovné (resp. že: $S=\frac{or}{2}$). Tyto dvě geometrické definice mohou narazit na problémy v oblastech matematiky, která jindy geometrii nepoužívá. Z tohoto důvodu matematici často dávají přednost definici π bez geometrie. Využívají k tomu matematickou analýzu. Často se π definuje jako dvojnásobek nejmenší kladné hodnoty x, pro kterou je goniometrická funkce cos(x) rovna nule.

Iracionálnost a transcendentnost

π je iracionální číslo, což znamená, že ho nelze vyjádřit podílem dvou celých čísel. Je to také transcendentní číslo, což znamená, že neexistuje polynom s racionálními koeficienty, pro který by π bylo kořenem. Jedním z důsledků transcendentnosti je, že π nelze zkonstruovat kružítkem a pravítkem (euklidovsky). Protože souřadnice všech bodů, které mohou být konstruovány eukleidovskou konstrukcí, jsou konstruovatelná čísla, nelze např. provést kvadraturu kruhu, což znamená, že pouze pomocí kružítka a pravítka nelze zkonstruovat čtverec, jehož obsah je stejný jako obsah daného kruhu. To je důležitý důkaz, protože kvadratura kruhu je jeden z tří geometrických problémů pocházejících už z antického Řecka.

Vyjádření v desítkové soustavě

Prvních 50 desetinných míst π v desítkové soustavě je:

π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510…

Na různých internetových stránkách se vyskytuje mnohem více číslic čísla π. 14. března 2019 Emma Harukaová Iwaová představila hodnotu π na 31,416 bilionů desetinných míst. Výpočet trval 121 dní na 25 počítačích.Tento počin je zapsán v Guinnessově knize rekordů. I když bylo π spočítáno na více než bilion (10¹²) číslic, v aplikované matematice se většinou používá zaokrouhlení pouze na několik desítek desetinných míst. Například 11 desetinných míst π stačí na odhad délky kružnice, která je velká jako Země, s chybou menší než jeden milimetr a 39 desetinných míst stačí na jakoukoli představitelnou aplikaci. NASA ve svých výpočtech používá 15 desetinných míst.

Protože π je iracionální číslo, číslice v jeho desetinném rozvoji se nikdy nezačnou opakovat. Sled těchto číslic fascinuje matematiky i laiky a během posledních pár století se vkládají snahy do vypočítání více číslic π a zkoumání jeho vlastností. Zatím se ale nepodařilo najít žádný vzor, podle kterého by se číslice opakovaly.

Odhad π

Číselná soustava	Aproximace $\pi$
Dvojková	11,00100 10000 11111 10110…
Osmičková	3,11037 55242 10264 30215…
Desítková	3,14159 26535 89793 23846 26433 83279 50288…
Šestnáctková	3,243F6 A8885 A308D 31319…
Racionální aproximace	3, Šablona:Zlomek, Šablona:Zlomek, Šablona:Zlomek, Šablona:Zlomek, … (seřazeno od méně přesné k přesnější aproximaci)
Řetězový zlomek	Šablona:Nowrap (Tento zlomek není periodický. Zobrazeno v lineárním zápisu.)

1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959

Prvních 1120 desetinných míst čísla π správně určili v roce 1948 John Wrench a Levi Smith pomocí kalkulačky. Byl to nejpřesnější odhad π před příchodem počítačů.

Nejhrubější odhad π je 3. Tato hodnota může stačit u případů, kde není potřeba lepší přesnosti než 5 %. Je to poměr obvodu vepsaného pravidelného šestiúhelníku k průměru kružnice.

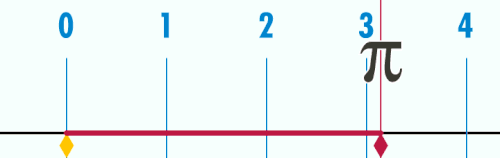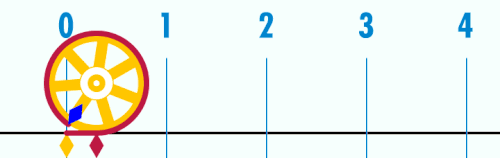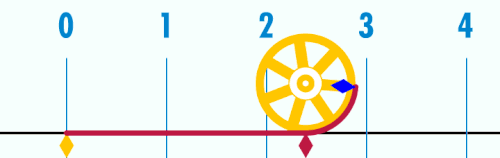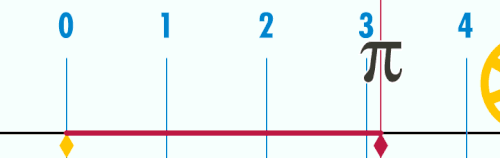
π se dá odhadnout narýsováním kružnice, změřením jejího průměru a její délky a následným vydělením délky průměrem.

Další způsob, který navrhl Archimédés, je spočítat obvod o_n pravidelných mnohoúhelníků vepsaných a opsaných kružnici o průměru d a postupně zdvojnásobit počet stran obou mnohoúhelníků. Porovnáním obvodu vepsaného a opsaného mnohoúhelníku lze odhadnout přesnost takto odhadnutého čísla π. Archimédés začínal s šestiúhelníky a skončil u mnohoúhelníků s 96 stranami a spočítal rozsah, v němž π leží:

π lze také spočítat čistě matematickými metodami. Protože je transcendentní, nelze ho vyjádřit pomocí algebraické rovnice, v níž by se vyskytovaly jen racionální koeficienty. Vyjádření pomocí elementární aritmetiky často obsahuje řady nebo sumační značení (např. „…“), což naznačuje, že vzorec je ve skutečnosti vzorcem pro nekonečnou řadu aproximací π. Čím více prvků sumace obsahuje, tím přesnější bude odhad.

Vzorce k vypočítání π mají požadované matematické vlastnosti, ale jsou těžko pochopitelné bez znalosti trigonometrie. Některé jsou ale jednodušší, například Leibnizova řada:

I když je tuto řadu jednoduché napsat a spočítat, nemusí být zpočátku jasné, proč je její výsledek π. Navíc je tak zdlouhavá, že je potřeba téměř 300 prvků, aby vyšla správně první dvě desetinná místa π. Když se ale řada upraví, lze π počítat mnohem rychleji. Vezměme si posloupnost

${\pi }_{0,1}=\frac{4}{1},{\pi }_{0,2}=\frac{4}{1}-\frac{4}{3},{\pi }_{0,3}=\frac{4}{1}-\frac{4}{3}+\frac{4}{5},{\pi }_{0,4}=\frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7},\cdots$

a poté definujme

${\pi }_{i,j}=\frac{{\pi }_{i-1,j}+{\pi }_{i-1,j+1}}{2}\text{ pro }i,j\ge 1.$

Poté výpočet ${\pi }_{10,10}$ zabere stejně času, jako výpočet 150 prvků původní řady, a ${\pi }_{10,10}=3.141592653\dots$, což je správnost na 9 desetinných míst. Tato úprava se nazývá van Wijngaardenova transformace.

Aproximace 355/113 (3,1415929…), která dává správně prvních 7 číslic π, se dá získat ze řetězového zlomku a je to nejlepší aproximace π vyjádřená zlomkem s maximálně čtyřcifernými čísly; další lepší aproximace je až 52163/16604 (3,141592387…).

Historie

Starověk

O znalosti π se spekuluje již u starověkých Egypťanů v období Staré říše, a to na základě rozměrů pyramid, ve kterých je údajně zakódováno. Velká pyramida v Gíze zkonstruovaná někdy mezi lety 2589–2566 př. n. l. byla postavena s obvodem 1760 loktů a s výškou 280 loktů; poměr 1760/280 = 44/7 ≈ 2π. Stejné proporce byly zvoleny při dřívější stavbě pyramidy Meidum (zhruba 2613–2589 př. n. l.). Někteří egyptologové to považují za záměr architektů. Miroslav Verner napsal: „Můžeme usoudit, že i když Egypťané neuměli přesně určit hodnotu π, v praxi ho používali.“ Podobný názor zastával i William Flinders Petrie. Jiní tvrdí, že starověcí Egypťané o pí nevěděli a do svých staveb se ho tudíž nesnažili promítnout. Pyramidy mohly být stavěny jednoduše podle poměrů stran pravoúhlých trojúhelníků. Jinou možností je vysvětlení výskytu čísla pí jako důsledku použité metody měření (vytyčování vzdáleností). Délkové míry se měřily odvalením kola, výškové pak jeho přikládáním na sebe. Tímto dojde automaticky k promítnutí čísla pí do poměru výšky a strany pyramidy. Pyramida tak byla stavěna s jednoduchými mírami: 280 „výškových loktů“ a 280 „délkových loktů“.

Nejstarší písemně doložené odhady π se datují do doby okolo 1900 př. n. l.; jsou to 256/81 (Egypt) a 25/8 (Babylon), oba méně než 1 % vzdálené od skutečné hodnoty. Indický text Šatapatha Brahmana dává odhad 339/108 ≈ 3,139. Biblické pasáže v 1. knize královské 7,23 a 2. knize kronik 4,2 mluví o obřadním bazénu v paláci krále Šalomouna, který má průměr deset loktů a obvod třicet loktů; někteří z toho usuzují, že autoři přisuzovali pí hodnotu okolo tří, ale jiní se to snaží vysvětlit šestiúhelníkovým bazénem.

Archimédés používal k odhadu π metodu vyčerpání

Archimédés (287–212 př. n. l.) byl první, kdo odhadl π důsledně. Uvědomil si, že hodnota může být ohraničena shora i zespoda vepsáním a opsáním pravidelných mnohoúhelníků do kružnice a vypočtením jejich obvodů. Použitím 96úhelníků dokázal, že 223/71 < π < 220/70. Průměr těchto hodnot je zhruba 3,14185.

Ptolemaios udává ve svém Almagestu hodnotu 3,14167, kterou možná získal od Apollónia z Pergy.

Okolo roku 265 poskytl Liou Chuej, matematik z říše Cchao Wej, jednoduchý a důsledný opakující se algoritmus pro výpočet π s libovolnou přesností. Sám vypočítal hodnotu pro 3072úhelník a získal hodnotu 3,1416. Později vynalezl rychlejší metodu, kterou získal hodnotu 3,14 s použitím 96úhelníku.>

Okolo roku 480 čínský matematik Cu Čchung-č’ pomocí metody Liou Chueje ukázal, že π ≈ 355/113 a 3,1415926 < π < 3,1415927. Použil k tomu 12288úhelník. Tato hodnota zůstala nejpřesnější dlouhých 900 let.

Druhé tisíciletí

Ruční výpočty

Ve 12. století prohlásil Maimonides, že π je iracionální. To bylo dokázáno v roce 1761 Johannem Heinrichem Lambertem. Během 20. století byly nalezeny důkazy, které vyžadují pouze znalosti integrálu. Jeden z nich proslavil Ivan Niven. Podobný důkaz ukázala o něco dříve Mary Cartwright.

Do 2. tisíciletí bylo π spočítáno na méně než 10 desetinných míst. Další výrazný pokrok v odhadování jeho hodnoty přišel s vývojem nekonečných řad a diferenciálního a integrálního počtu. Od té doby bylo možné π spočítat s jakoukoli přesností pomocí řad. Okolo roku 1400 vymyslel Madhava ze Sangamagramy první nám známou takovou řadu:

$\pi =4\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{2k+1}=\frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}+\cdots$

Tato řada je známá jako Madhavova-Leibnizova řada nebo Gregoryho-Leibnizova řada, protože ji znovuobjevili James Gregory a Gottfried Leibniz v 17. století. Postup je ovšem tak pomalý, že je potřeba spočítat 4000 prvků, aby byl výsledek přesnější než ten Archimédův. Ale po úpravě řady na

$\begin{array}{cc}\pi & =\sqrt{12}\sum _{k=0}^{\mathrm{\infty }}\frac{(-3{)}^{-k}}{2k+1}=\sqrt{12}\sum _{k=0}^{\mathrm{\infty }}\frac{(-\frac{1}{3}{)}^k}{2k+1}\\ & =\sqrt{12}(1-\frac{1}{3\cdot 3}+\frac{1}{5\cdot 3^2}-\frac{1}{7\cdot 3^3}+\cdots ),\end{array}$

byl Madhava schopen π odhadnout na 3,14159265359, což je správně na 11 desetinných míst. Tento rekord pokořil v roce 1424 perský matematik Al-Káší, který ho odhadl na 16 desetinných míst.

V Evropě po Archimédovi udělal další velký pokrok německý matematik Ludolph van Ceulen (1540–1610), který použil geometrickou metodu, díky které odhadl π správně na 35 desetinných míst. Na svůj výpočet byl tak hrdý, že si tuto hodnotu nechal vytesat na hrob. Pí se proto někdy nazývá Ludolfovým číslem.

Někdy v té době se v Evropě začala vyvíjet metoda nekonečných řad. První takové vyjádření nabízel nekonečný součin, který v roce 1593 vymyslel François Viète:

Dalším známým vyjádřením je Wallisův součin od Johna Wallise z roku 1655:

$\frac{\pi }{2}=\prod _{k=1}^{\mathrm{\infty }}\frac{(2k{)}^2}{(2k{)}^2-1}=\frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdot \frac{8}{7}\cdot \frac{8}{9}\cdots =\frac{4}{3}\cdot \frac{16}{15}\cdot \frac{36}{35}\cdot \frac{64}{63}\cdots .$

Isaac Newton v letech 1665–66 odvodil vzorec pomocí řady s arkem sinem a vypočítal π na 15 číslic:

$\begin{array}{cc}\pi & =6\arcsin \frac{1}{2}\\ & =6(\frac{1}{2^1\cdot 1}+\left(\frac{1}{2}\right)\frac{1}{2^3\cdot 3}+\left(\frac{1\cdot 3}{2\cdot 4}\right)\frac{1}{2^5\cdot 5}+\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)\frac{1}{2^7\cdot 7}+\cdots )\\ & =3\sum _{n=0}^{\mathrm{\infty }}\frac{(\genfrac{}{}{0ex}{}{2n}{n})}{16^n(2n+1)}\\ & =3+\frac{1}{8}+\frac{9}{640}+\frac{15}{7168}+\frac{35}{98304}+\frac{189}{2883584}+\frac{693}{54525952}+\frac{429}{167772160}+\cdots .\end{array}$

Později ale prohlásil: „Stydím se říci, na kolik číslic jsem tyto výpočty prováděl, když jsem zrovna neměl co jiného na práci.“ Tento výpočet se k π přibližuje lineárně s rychlostí μ, která je alespoň tři desetinná místa na každých pět prvků. Když se n blíží k nekonečnu, μ se blíží k 1/4 a 1/μ ke 4:

$\mu =\frac{(2n-1{)}^2}{8n(2n+1)};\frac{1}{\mu }=\frac{8n(2n+1)}{(2n-1{)}^2}$.

V roce 1706 se povedlo Johnu Machinovi jako prvnímu spočítat π na 100 desetinných míst. Použil k tomu řadu s arkem tangens

$\arctan x=\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k{x}^{2k+1}}{2k+1}=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots$

a vymyslel vzorec

$\frac{\pi }{4}=4\arctan \frac{1}{5}-\arctan \frac{1}{239}.$

Vzorce podobného typu se až do příchodu počítačů staly nejlepší možnou metodou výpočtu π. Johann Dase, jeden z takzvaných lidských kalkulátorů, v roce 1844 pomocí podobné rovnice v hlavě vypočítal 200 desetinných míst π. Na konci 19. století držel rekord William Shanks, který za 15 let vypočítal 707 číslic π, i když kvůli chybě bylo jen 527 z nich správně. (Novější rekordy jsou často počítány dvakrát dvěma různými rovnicemi, aby se zabránilo takovýmto chybám. Když se výsledky shodují, jsou nejspíše správné.)

Teoretický pokrok 18. století vedl k několika objevům o povaze π, které jsou neproveditelné pouze pomocí číselných výpočtů. V roce 1761 dokázal Johann Heinrich Lambert iracionalitu π a v roce 1794 dokázal Adrien-Marie Legendre, že i π² je iracionální. Když Leonhard Euler v roce 1735 vyřešil známý Basilejský problém a zjistil, že hodnota Riemannovy funkce zeta pro 2 je

$\zeta (2)=\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^2}=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots$

neboli π²/6, prokázal, že π má spojitost s prvočísly. Legendre i Euler navrhli, že π by mohlo být transcendentní číslo, což v roce 1882 dokázal Ferdinand von Lindemann.

Výpočet v počítačové éře

Počítačová animace π

Příchod počítačů ve 20. století vedl k novým a novým rekordům ve výpočtu π. John von Neumann se svým týmem v roce 1949 použil ENIAC k výpočtu prvních 2037 číslic π, což počítači zabralo 70 hodin. V příštích desetiletích byly přidány tisíce desetinných míst a hranice milionu číslic byla překonána v roce 1973. Pokrok nebyl rychlejší než předtím jen kvůli rychlejšímu hardware, ale i díky novým algoritmům. Jedním z největších pokroků byl objev rychlé Fourierovy transformace (FFT) v šedesátých letech, který umožňuje počítačům velmi rychle provádět výpočty s velkými čísly.

Na začátku 20. století vymyslel indický matematik Šrínivása Rámanudžan několik nových vzorců pro π, z nichž některé jsou pozoruhodné svou elegancí, hloubkou a rychlostí konvergence. Jeden z jeho vzorců je řada

$\frac{1}{\pi }=\frac{2\sqrt{2}}{9801}\sum _{k=0}^{\mathrm{\infty }}\frac{(4k)!(1103+26390k)}{(k!{)}^{4}396^{4k}},$

kde k! je faktoriál k.

Několik dalších je ukázáno v následující tabulce:

$\pi =\frac{1}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{((2n)!{)}^3(42n+5)}{(n!{)}^6{16}^{3n+1}}$
$\pi =\frac{4}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n(4n)!(21460n+1123)}{(n!{)}^4{441}^{2n+1}{2}^{10n+1}}$
$\pi =\frac{4}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(6n+1){\left(\frac{1}{2}\right)}_n^3}{4^n(n!{)}^3}$
$\pi =\frac{32}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}{\left(\frac{\sqrt{5}-1}{2}\right)}^{8n}\frac{(42n\sqrt{5}+30n+5\sqrt{5}-1){\left(\frac{1}{2}\right)}_n^3}{64^n(n!{)}^3}$
$\pi =\frac{27}{4Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}{\left(\frac{2}{27}\right)}^n\frac{(15n+2){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{3}\right)}_n{\left(\frac{2}{3}\right)}_n}{(n!{)}^3}$
$\pi =\frac{15\sqrt{3}}{2Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}{\left(\frac{4}{125}\right)}^n\frac{(33n+4){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{3}\right)}_n{\left(\frac{2}{3}\right)}_n}{(n!{)}^3}$
$\pi =\frac{85\sqrt{85}}{18\sqrt{3}Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}{\left(\frac{4}{85}\right)}^n\frac{(133n+8){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{6}\right)}_n{\left(\frac{5}{6}\right)}_n}{(n!{)}^3}$
$\pi =\frac{5\sqrt{5}}{2\sqrt{3}Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}{\left(\frac{4}{125}\right)}^n\frac{(11n+1){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{6}\right)}_n{\left(\frac{5}{6}\right)}_n}{(n!{)}^3}$
$\pi =\frac{2\sqrt{3}}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(8n+1){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{4}\right)}_n{\left(\frac{3}{4}\right)}_n}{(n!{)}^3{9}^n}$
$\pi =\frac{\sqrt{3}}{9Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(40n+3){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{4}\right)}_n{\left(\frac{3}{4}\right)}_n}{(n!{)}^3{49}^{2n+1}}$
$\pi =\frac{2\sqrt{11}}{11Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(280n+19){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{4}\right)}_n{\left(\frac{3}{4}\right)}_n}{(n!{)}^3{99}^{2n+1}}$
$\pi =\frac{\sqrt{2}}{4Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(10n+1){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{4}\right)}_n{\left(\frac{3}{4}\right)}_n}{(n!{)}^3{9}^{2n+1}}$
$\pi =\frac{4\sqrt{5}}{5Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(644n+41){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{4}\right)}_n{\left(\frac{3}{4}\right)}_n}{(n!{)}^3{5}^n{72}^{2n+1}}$
$\pi =\frac{4\sqrt{3}}{3Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n(28n+3){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{4}\right)}_n{\left(\frac{3}{4}\right)}_n}{(n!{)}^3{3}^n{4}^{n+1}}$
$\pi =\frac{4}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n(20n+3){\left(\frac{1}{2}\right)}_n{\left(\frac{1}{4}\right)}_n{\left(\frac{3}{4}\right)}_n}{(n!{)}^3{2}^{2n+1}}$
$\pi =\frac{72}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n(4n)!(260n+23)}{(n!{)}^4{4}^{4n}18^{2n}}$
$\pi =\frac{3528}{Z}$	$Z=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n(4n)!(21460n+1123)}{(n!{)}^4{4}^{4n}882^{2n}}$

Z podobného vzorce, který v roce 1987 vymysleli bratři Čudnovští,

$\frac{426880\sqrt{10005}}{\pi }=\sum _{k=0}^{\mathrm{\infty }}\frac{(6k)!(13591409+545140134k)}{(3k)!(k!{)}^3(-640320{)}^{3k}}$

lze získat 14 číslic na jeden prvek. Pomocí něho bratři ke konci osmdesátých let vytvořili několik rekordů ve výpočtu π včetně pokoření hranice jedné miliardy číslic (konkrétně 1 011 196 691) v roce 1989. Tato metoda se používá na výpočet π v programech na dnešních osobních počítačích. 5. října 2010 oznámil PhysOrg.com, že počítačoví experti Shigeru Kondo a Alexander Yee vypočítali π na pět bilionů desetinných míst, čímž dvojnásobně překonali předchozí rekord. Později rekord navýšili na deset a dvanáct bilionů.

Většina řad zvyšuje přesnost výpočtu s pevně danou rychlostí, ale existují algoritmy, které násobí počet správných číslic s každým krokem. V roce 1975 matematici Richard Brent a Eugene Salamin objevili Brentův-Salaminův algoritmus, který s každým dalším krokem počet správných číslic zdvojnásobí. Nejdříve se definují proměnné

$a_0=1b_0=\frac{1}{\sqrt{2}}{t}_0=\frac{1}{4}{p}_0=1$

a poté se opakuje

$a_{n+1}=\frac{a_n+b_n}{2}{b}_{n+1}=\sqrt{a_n{b}_n}$

$t_{n+1}=t_n-p_n(a_n-a_{n+1}{)}^2{p}_{n+1}=2p_n$

dokud a_n a b_n nemají podobnou hodnotu. Potom lze π odhadnout následovně:

$\pi \approx \frac{(a_n+b_n{)}^2}{4t_n}.$

25 opakování tohoto algoritmu vede ke 45 milionům správných desetinných míst. Podobný algoritmus, který každým krokem zečtyřnásobuje přesnost, objevili Jonathan a Peter Borweinovi. Tyto metody použil Jasumasa Kanada se svým týmem k dosažení většiny rekordů v odhadu π od roku 1980. Nejpřesnějšího výsledku do konce 2. tisíciletí dosáhl roku 1999, kdy π vypočítal na 206 158 430 000 desetinných míst.

V roce 1995 Simon Plouffe vyvinul Baileyho-Borweinův-Plouffeův vzorec (BBP vzorec):

Tento vzorec je zajímavý tím, že dokáže určit n-tou binární hodnotu π bez počítání těch předchozích. V roce 2000 se zjistilo, že biliardtý bit π má hodnotu 0.

V roce 1997 objevil matematik Fabrice Bellard tzv. Bellardův vzorec:Šablona:Vzorec

Tento vzorec je zajímavý tím, že je na výpočet přibližně o 43% rychlejší než BBP vzorec.

V březnu 2019 byl publikován tehdejší rekord v nejpřesnějším odhadu π v desítkové soustavě, který má 31,4 bilionu číslic. Spočítala jej japonská počítačová specialistka Emma Haruka Iwao s využitím výpočetní síly cloudu společnosti Google. Aktuálně nejpřesnější odhad (červen 2024) má 202 biliony desetinných míst.

Pí a řetězový zlomek

Čísla v tomto vyjádření π v nekonečném řetězovém zlomku nevykazují žádnou pravidelnost: Šablona:Vzorec neboli Šablona:Vzorec

Existují ale zobecněné řetězové zlomky pro výpočet π, které mají pravidelnou strukturu, například tento:

$\pi =\frac{4}{1+\frac{1^2}{2+\frac{3^2}{2+\frac{5^2}{2+\frac{7^2}{2+\frac{9^2}{2+\ddots }}}}}}=3+\frac{1^2}{6+\frac{3^2}{6+\frac{5^2}{6+\frac{7^2}{6+\frac{9^2}{6+\ddots }}}}}=\frac{4}{1+\frac{1^2}{3+\frac{2^2}{5+\frac{3^2}{7+\frac{4^2}{9+\ddots }}}}}$

Otevřené otázky

Jedna otevřená otázka o π je ta, jestli je to normální číslo – jestli se jakákoli řada čísel v jeho rozvoji objevuje tak často, jak se statisticky předpokládá u „náhodné“ řady čísel.

Další otázkou je, jestli je množina {π, e} algebraicky nezávislá, i když Jurij Nesterenko v roce 1996 dokázal, že množina {π, e^π, Γ(1/4)} algebraicky nezávislá je.

Použití v matematice a ve vědě

π se hojně objevuje v rovnicích v matematice, vědě a inženýrství. Objevuje se i tam, kde se nevyskytuje žádná zřetelná spojitost s kruhy eukleidovské geometrie.

Geometrie a goniometrie

Pro každý kruh s poloměrem r a průměrem d = 2r platí, že jeho obvod je πd a obsah πr². Dále se π objevuje v rovnicích pro výpočet obsahů a objemů pro mnoho geometrických útvarů, jejichž tvary jsou založené na kružnicích, například elipsy, koule, kužely a tory. Proto se vyskytuje i v určitých integrálech, které popisují obvod, obsah nebo objem útvarů vytvářených kruhy. Například polovina plochy jednotkového kruhu je vyjádřena integrálem: $\underset{-1}{\overset{1}{\int }}\sqrt{1-x^2}\mathrm{d}x=\frac{\pi }{2}$ a

$\underset{-1}{\overset{1}{\int }}\frac{1}{\sqrt{1-x^2}}\mathrm{d}x=\pi$

vyjadřuje polovinu délky jednotkové kružnice. Lze integrovat i složitější tělesa, např. rotační tělesa.

Z definice goniometrických funkcí pomocí jednotkové kružnice vyplývá, že sinus a kosinus mají periodu 2π. To znamená, že pro každé x a celé číslo n platí sin(x) = sin(x + 2πn) a cos(x) = cos(x + 2πn), protože sin(0) = 0, sin(2πn) = 0 pro všechna celá čísla n. Z definice také plyne, že 180° je rovno π radiánům, neboli 1° = (π/180) radiánů.

V moderní matematice je π často definováno pomocí goniometrických funkcí, například jako nejmenší kladné x, pro které platí sin x = 0. Dělá se to kvůli odstranění závislosti na eukleidovské geometrii. π může být také definováno pomocí cyklometrických funkcí, např. π = 2 arccos(0) nebo π = 4 arctan(1). Rozšíření cyklometrických funkcí jako mocninných řad je nejjednodušší způsob, jak odvodit nekonečné řady pro π.

Komplexní čísla

Eulerův vzorec zobrazuje komplexní rovina. Zvýšení úhlu φ na π radiánů (180°) vede k Eulerově rovnosti

Komplexní číslo $z$ lze vyjádřit v polární soustavě souřadnic následovně:

$z=r\cdot (\cos \phi +\mathrm{i}\sin \phi )$

Častý výskyt π v komplexní analýze může mít spojitost s chováním exponenciální funkce komplexní proměnné popsané Eulerovým vzorcem

${\mathrm{e}}^{\mathrm{i}\phi }=\cos \phi +\mathrm{i}\sin \phi$

kde i je imaginární jednotka, pro kterou platí i² = −1, a e ≈ 2,71828 je Eulerovo číslo. Tento vzorec naznačuje, že imaginární mocniny e popisují rotaci na jednotkové kružnici v komplexní rovině; tyto rotace mají periodu 360° = 2π. Když se úhel φ rovná π, vznikne Eulerova rovnost

${\mathrm{e}}^{\mathrm{i}\pi }=-1.$

${\mathrm{e}}^{\mathrm{i}\pi }+1=0$

Eulerova rovnost je známá díky spojení několika základních matematických pojmů do jednoho krátkého elegantního vzorce.

Existuje n různých n-tých odmocnin jedničky

${\mathrm{e}}^{2\pi \mathrm{i}k/n}(k=0,1,2,\dots ,n-1).$

Pravděpodobnost a statistika

V pravděpodobnosti a statistice se vyskytuje několik vzorců, které obsahují π.

• Pravděpodobnost, že 2 náhodně zvolená celá čísla jsou nesoudělná, je $\frac{6}{{\pi }^2}$.
• Funkce hustoty pravděpodobnosti pro normální rozdělení, kde μ je střední hodnota a σ je směrodatná odchylka:

$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-(x-\mu {)}^2/(2{\sigma }^2)}$.

• Funkce hustoty pravděpodobnosti pro (standardní) Cauchyho rozdělení:

$f(x)=\frac{1}{\pi (1+x^2)}.$

Se znalostí faktu, že pro libovolnou hustotu pravděpodobnosti platí, že $\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)dx=1$, lze z předchozích vzorců odvodit další vzorce pro výpočet čísla π.

Buffonova jehla je úloha, díky které je možné empiricky odhadnout hodnotu π. Představme si, že máme jehlu o délce L jednotek, kterou opakovaně házíme na povrch, jež je rozdělen rovnoběžnými linkami od sebe vzdálenými S jednotek (s tím, že S > L). Pokud je jehla hozena n–krát a x–krát z toho překříží linku (x > 0), potom lze π přibližně odhadnout pomocí metody Monte Carlo:

$\pi \approx \frac{2nL}{xS}.$

I když je tato metoda matematicky dokonalá, nelze s ní určit hodnotu π pomocí experimentu na více než pár číslic. Správné určení pouze tří prvních číslic (3,14) vyžaduje miliony hodů a počet hodů roste exponenciálně s počtem požadovaných číslic.

Některé důležité vztahy z dalších oborů matematiky

• Gaussův integrál

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\mathrm{e}}^{-x^2}\mathrm{d}x=\sqrt{\pi }.$

Důsledkem toho je, že gama funkce poloviny celého čísla je racionálním násobkem √π, např.:

$\mathrm{\Gamma }\left(\frac{1}{2}\right)=\sqrt{\pi }$

• Stirlingův vzorec

$n!\sim \sqrt{2\pi n}{\left(\frac{n}{\mathrm{e}}\right)}^n$

• Cauchyův vzorec

$f(z_0)=\frac{1}{2\pi \mathrm{i}}{\oint }_c\frac{f(z)\mathrm{d}z}{z-z_0}$

Fyzika

I když π není fyzikální konstanta, objevují se ve fyzikálních vztazích koeficienty obsahující $\pi$, které vyjadřují jistou geometrickou symetrii (2$\pi$ pro kruhovou či válcovou symetrii – plný rovinný úhel v obloukové míře, 4$\pi$ pro kulovou symetrii – plný prostorový úhel). Volbou jednotek koeficient sice může zmizet u jednoho vztahu, ale objeví se u jiného, takže plně se ho zbavit nelze. Některé soustavy jednotek (například soustava SI pro elektromagnetické jednotky) proto respektují tzv. racionalizaci, tzn. že koeficienty obsahující $\pi$ se vyskytují pouze v těch vztazích, kde jsou geometricky a fyzikálně oprávněné. Níže uvedený vzorec pro Coulombovu sílu (všesměrové působení do plného prostorového úhlu) proto koeficient 4$\pi$ obsahuje „oprávněně“, jeho eliminace (např. v Gaussově soustavě jednotek CGS) pak vede k „podivným“ koeficientům 4$\pi$ ve vztazích pro elektrickou indukci a v Maxwellových rovnicích. Ze stejného důvodu se objevuje faktor 2·4$\pi$ v níže uvedené Einsteinově rovnici, neboť vztah pro Newtonův gravitační zákon je tradičně neracionalizovaný.

Koeficienty 2$\pi$ se vyskytují i u některých rovnic periodických dějů. Je to proto, že fáze jedné periody se tradičně pokládá rovna 2$\pi$, tedy plnému úhlu, aby byla zajištěna korespondence průmětu rovnoměrného pohybu po kružnici do jedné osy souřadné s harmonickým kmitavým pohybem. (Zde je i původ 2$\pi$ v níže uvedené relaci neurčitosti, použije-li se namísto „přirozené“ modifikované Planckovy konstanty konstanta nemodifikovaná.)

Hodnotu lze získat i z různých experimentů a pozorování.

Příklady:

• Heisenbergův princip neurčitosti, který ukazuje, že nepřesnosti měření polohy částice (Δx) a hybnosti (Δp) nemohou být zároveň libovolně malé:

$\mathrm{\Delta }x\mathrm{\Delta }p\ge \frac{h}{4\pi }=\frac{\hslash }{2}$

• Einsteinovy rovnice gravitačního pole v obecné teorii relativity:

$R_{ik}-\frac{g_{ik}R}{2}+\mathrm{\Lambda }{g}_{ik}=\frac{8\pi G}{c^4}{T}_{ik}$

• Kosmologická konstanta Λ z Einsteinovy rovnice gravitačního pole je ve vztahu s hustotou energie vakua ρ_vac následovně (G je gravitační konstanta):

$\mathrm{\Lambda }=8\pi G{\rho }_{\text{vac}}$

• Coulombův zákon pro výpočet elektrické síly mezi dvěma elektrickými náboji (q₁ a q₂) od sebe vzdálených délkou r (ε₀ vyjadřuje permitivitu vakua):

$F=\frac{\left|q_1{q}_2\right|}{4\pi {\epsilon }_0{r}^2}$

• Ampérův vzorec pro magnetickou sílu působící na délce $l$ mezi dvěma rovnoběžnými vodiči vzdálenými od sebe o kolmou vzdálenost $d$ protékanými proudy $I_1$, $I_2$:

$\frac{F}{l}=\frac{{\mu }_0}{2\pi }\frac{I_1{I}_2}{d}$

• 3. Keplerův zákon týkající se doby oběhu (T), velké poloosy dráhy (a) a hmotností (M a m):

${\left(\frac{2\pi }{T}\right)}^2{a}^3={\omega }^2{a}^3=G(M+m)$

Memorování číslic

Nynější světový rekord v Guinnessově knize rekordů drží Rajveer Meena z Indie se 70 000 zapamatovanými číslicemi. Trvalo mu to 9 hodin 27 minut, dne 21. března 2015. Nahradil tak Číňana Lu Chao, který měl 67 890 zapamatovaných číslic. Recitování mu v roce 2005 trvalo 24 hodin a 4 minuty. Rekord japonského inženýra Akira Haragučiho 100 000 číslic nebyl zatím Guinnessovou knihou uznán.

Existuje několik způsobů zapamatování si co nejvíce číslic desetinného rozvoje π, například tzv. piemy, což jsou básně, kde délka každého slova reprezentuje číslici. Báseň Cadaeic Cadenza takto vyjadřuje prvních 3834 číslic. Existují i různé mnemotechnické pomůcky, díky kterým si lze několik číslic π zapamatovat:

• Sám u sebe v hlavě magického pí číslic deset mám. (9 za desetinnou čárkou)
• Lín a kapr u hráze prohlídli si rybáře, udici měl novou, jikrnáči neuplovou. (12 za desetinnou čárkou.) Jiná verze Rak a kapr u hráze pohleděli na rybáře, udici měl novou, šupináči neuplavou.
• Dej, ó Bože, a číslo Ludolfovo já navždy pomnu, pro větší naplnění moudrosti početní. (13 číslic za desetinnou čárkou)
• Mám ó bože ó velký pamatovat si takový cifer řád, velký slovutný Archimedes, pomáhej trápenému, dej mu moc, nazpaměť nechť odříká ty slavné sice, ale tak protivné nám, ach, číslice Ludolfovy! (30 číslic za desetinnou čárkou)

Odraz v kultuře

Číslu π je věnována oslava na den pí – 14. března (v americkém zápise MM-DD-RRRR je den označen 3/14, tj. první desetinná místa čísla π).

Odkazy

Literatura

• Šablona:Citace monografie

Externí odkazy

• Šablona:Commonscat
• Šablona:Wikislovník
• Šablona:En http://numbers.computation.free.fr/Constants/Pi/pi.html
• Šablona:En Digits of Pi na Open Directory Project
• Šablona:En Formulas for π na MathWorld
• Šablona:En Representations of Pi na Wolfram Alpha
• Šablona:En Pi Šablona:Wayback na PlanetMath
• Šablona:En Determination of π na Cut-the-knot
• Šablona:En Statistical Distribution Information on PI based on 1.2 trillion digits of PI
• Šablona:En Pi Search Engine (2 billion digits)
• Šablona:En Pi is Wrong!
• Šablona:En The Tau Manifesto.
• Šablona:En A000796 v OEIS