Arkus kosinus

Grafy funkcí arkus sinus a arkus kosinus

Arkus kosinus je jedna z cyklometrických funkcí, inverzní funkce k funkci kosinus. Obvykle se značí $\arccos x$, v anglické literatuře se taktéž používá $\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{s}x$ či ${\cos }^{-1}x$. Její hodnotou je úhel v obloukové míře (radiány) z intervalu $⟨0,\pi ⟩$, jehož kosinus je $x$.

Definice

Funkce $y=\arccos x$ je inverzní k funkci $x=\cos y(0\le y\le \pi )$; je definována pro $x\in ⟨-1,1⟩$.

Vlastnosti

Značení:	$y=\arccos x$ $(\text{resp.}\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{s}x,{\cos }^{-1}x)$
Definiční obor	$⟨-1,1⟩$
Obor hodnot	$⟨0,\pi ⟩$
Omezenost	Je omezená
Monotonie	Je ryze klesající $⟹$ je prostá
Symetrie	Není lichá ani sudá, ale graf je souměrný podle středu $(x,y)=(0,\frac{\pi }{2})$
Periodicita	Není periodická
Limity	$\underset{x\to 0}{\lim }\frac{\frac{\pi }{2}-\arccos x}{x}=1$ tj. v okolí nuly je $\text{arccos }x\approx (\frac{\pi }{2}-x)$
Inverzní funkce	$x=\cos y$   (kosinus)
Derivace	$(\arccos x{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}$
Integrál	$\int \arccos x\mathrm{d}x=x\arccos x-\sqrt{1-x^2}+C$
Taylorova řada	$\arccos x=\frac{\pi }{2}-x-\frac{1}{2}\frac{x^3}{3}-\frac{1\cdot 3}{2\cdot 4}\frac{x^5}{5}-\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\frac{x^7}{7}-\dots |x|<1$
Významné hodnoty	$\begin{array}{cccccccccc}x& -1& -\frac{\sqrt{3}}{2}& -\frac{\sqrt{2}}{2}& -\frac{1}{2}& 0& \frac{1}{2}& \frac{\sqrt{2}}{2}& \frac{\sqrt{3}}{2}& 1\\ \arccos x& \pi & \frac{5\pi }{6}& \frac{3\pi }{4}& \frac{2\pi }{3}& \frac{\pi }{2}& \frac{\pi }{3}& \frac{\pi }{4}& \frac{\pi }{6}& 0\end{array}$

Vzorce

$\begin{array}{ccc}\arcsin x+\arccos x& =& \frac{\pi }{2}\\ \arccos x+\arccos (-x)& =& \pi \\ \arccos x+\arccos y& =& \{\begin{array}{cc}\arccos (xy-\sqrt{1-x^2}\sqrt{1-y^2}),& x+y\ge 0\\ 2\pi -\arccos (xy-\sqrt{1-x^2}\sqrt{1-y^2}),& x+y<0\end{array}\\ \arccos x-\arccos y& =& \{\begin{array}{cc}-\arccos (xy+\sqrt{1-x^2}\sqrt{1-y^2}),& x\ge y\\ \arccos (xy+\sqrt{1-x^2}\sqrt{1-y^2}),& x<y\end{array}\end{array}$

$\begin{array}{cccc}\arccos (\cos x)& =& x,& 0\le x\le \pi \\ \cos (\arccos x)& =& x\end{array}$

$\arccos x=\underset{x}{\overset{1}{\int }}\frac{\mathrm{d}t}{\sqrt{1-t^2}},0<x<1$

$\arccos x=\frac{\pi }{2}-\frac{x\sqrt{1-x^2}}{1-\frac{1\cdot 2\cdot x^2}{3-\frac{1\cdot 2\cdot x^2}{5-\frac{3\cdot 4\cdot x^2}{7-\frac{3\cdot 4\cdot x^2}{9-\frac{5\cdot 6\cdot x^2}{11-\dots }}}}}},|x|<1$

Příklad použití

Mějme goniometrickou rovnici:

$\begin{array}{ccc}2\cos x& =& 1\\ \cos x& =& \frac{1}{2}\\ x& =& \arccos \frac{1}{2}\\ x& =& \frac{\pi }{3}\end{array}$

S ohledem na periodicitu funkce $\cos x$ jsou řešením původní rovnice také hodnoty:

$\begin{array}{ccccccccc}\dots ,& \frac{-11\pi }{3},& \frac{-5\pi }{3},& \frac{\mathit{\pi }}{3},& \frac{7\pi }{3},& \frac{13\pi }{3},& \dots & \text{tj.}{x}_k=& \frac{\pi }{3}+2k\pi ,k\in \mathbb{Z}\\ \dots ,& \frac{-13\pi }{3},& \frac{-7\pi }{3},& \frac{-\pi }{3},& \frac{5\pi }{3},& \frac{11\pi }{3},& \dots & \text{tj.}{x}_k=& -\frac{\pi }{3}+2k\pi ,k\in \mathbb{Z}\end{array}$

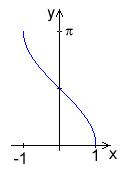
Graf

• Vznikne překlopením grafu funkce $y=\cos (x)$ podle osy I. a III. kvadrantu.

Graf funkce arkus kosinus

Odkazy

Externí odkazy

• Šablona:Commonscat
• BARTSCH, Hans-Jochen. Matematické vzorce. 3., rev. vyd. Přeložil Zdeněk TICHÝ. Praha: Mladá fronta, 1996. Šablona:ISBN.