Funkce (matematika)

Zobrazení z množiny M (nahoře) resp. množiny D (dole) na množinu T (přerušovaná čára) resp. do množiny T (plná čára).

Funkce je v matematice název pro zobrazení z množiny $M$ na nebo do číselného tělesa $T$ (množiny reálných nebo komplexních čísel), či na nebo do vektorového prostoru ${ℝ}^n$ tvořeného uspořádanými n-ticemi čísel v případě vektorové funkce. Je to tedy předpis, který každému prvku z množiny $D\subseteq M$ (kde množina $D$ se nazývá definiční obor funkce) přiřadí právě jedno číslo z množiny $T$ (kde množina resp. podmnožina $T$ se nazývá obor hodnot funkce).

V širším smyslu se pojem funkce někdy používá jako synonymum pro pojem zobrazení.

Definice

Funkce $f$ je binární relací $[f;D,T]$, kde každému prvku $x\in D$ je přiřazeno právě jedno číslo $y\in T$ tak, že $[x,y]\in f$ (jestliže $[x_1,y_1],[x_2,y_2]\in f$ a $x_1=x_2$, pak $y_1=y_2$). Místo $[x,y]\in f$ píšeme $y=f(x)$, kde $x$ nazýváme nezávisle proměnnou (argumentem) funkce $f$ a $y$ nazýváme závisle proměnnou (funkční hodnotou) funkce $f$.

Definičním oborem (doménou) funkce je podmnožina $D$ množiny $M$ všech prvků $x\in M$, ke kterým v relaci existuje právě jedna uspořádaná dvojice $[x,y]\in f$, kde $y\in T$.

Oborem hodnot (kodoménou) funkce je množina všech prvků $y\in T$, ke kterým v relaci existuje alespoň jedna uspořádaná dvojice $[x,y]\in f$, kde $x\in D$.

U prvků množiny $M$, které nejsou prvky definičního oboru $D$, říkáme, že funkce v nich není definována. Pokud není při zadání funkce uveden definiční obor $D$, pak se za něj obvykle považuje množina $M$ všech hodnot nezávisle proměnné, pro něž má funkce smysl. Definičním oborem může být například množina přirozených, celých, racionálních, reálných nebo komplexních čísel. Argumenty definičního oboru mohou mít obecně více dimenzí, pokud mají nekonečnou dimenzi, nemluvíme již o funkci, ale o funkcionálu.

Značení

Vektorovou funkci n reálných proměnných značíme $f:{ℝ}^n\to {ℝ}^m$, pak pro m=1 dostaneme $f:{ℝ}^n\to ℝ$, tj. reálná funkce více reálných proměnných a pro n=1 dostaneme $f:ℝ\to ℝ$, tj. reálná funkce reálné proměnné, kde zaměníme-li množinu reálných čísel $ℝ$ za množinu komplexních čísel $ℂ$, mluvíme o komplexní funkci komplexní proměnné.

Funkci n reálných proměnných dále značíme:

• $f(x_1,...,x_n)$
• $f(x_i)$ pro $i=1,...,n$
• $f(X)$, kde $X=[x_1,...,x_n]$ představuje bod v n-rozměrném prostoru
• $f(r)$, kde $r$ představuje polohový vektor bodu v n-rozměrném prostoru.

Zadání

Tabulkou (výčtem hodnot)

Funkci s diskrétním (oddělené hodnoty netvořící souvislý interval) oborem hodnot (ať už s diskrétním definičním oborem nebo funkci po částech konstantní) můžeme zadat výčtem hodnot, obvykle uspořádaným do tabulky.

Příklad

Příkladem může být zadání funkce např. tabulkou

$x$	1	2	5	7	9
$y$	2	4	5	3	3

Definičním oborem je zde množina $\{1,2,5,7,9\}$ a oborem hodnot je množina $\{2,3,4,5\}$.

Graficky

Grafickým zadáním funkci vyjádříme grafem.

Příklad

Příklad zadání funkce grafem ($D(x)$ označuje definiční obor a $V(y)$ obor hodnot)

Zadání funkce grafem.

Analyticky

Analytickým zadáním, tj. předpisem, rozumíme buďto explicitní vyjádření funkce ve tvaru $y=f(x)$, nebo implicitní vyjádření funkce ve tvaru $F(x,y)=0$. Dalším způsobem zadání funkce je vyjádření v parametrickém tvaru soustavou rovnic $x=f_1(t)$, $y=f_2(t)$, kde $t$ je vhodný parametr.

Příklad

Např. $y=2x^2$ je explicitní zápis kvadratické funkce. V implicitním tvaru lze stejnou funkci zapsat rovnicí $y-2x^2=0$. Pro vyjádření v parametrickém tvaru lze zvolit např. soustavu rovnic $x=\frac{t}{\sqrt{2}}$, $y=t^2$.

Rekurentně

Rekurentním zadáním, tj. předpisem, který dává do vztahu nějaké hodnoty funkce s jinými hodnotami funkce takovým způsobem, že funkce je dobře definována.

Příklad

Příkladem takové funkce může být např. funkce definovaná na přirozených číslech, kterou definujeme vztahy $f(0)=1$ a $f(n)=n\cdot f(n-1)$ pro $n=1,2,3,\cdots$.

Uvedenou funkci lze také zapsat jako $f(n)=n!$, tj. tato funkce počítá faktoriál čísla $n$. Rekurzivní funkce našly uplatnění především ve výpočetní technice.

Průběh

Vyšetřujeme-li průběh funkce, zkoumáme vlastnosti (graf) funkce, tj. hledáme body, které graf funkce dělí na intervaly mající příslušnou vlastnost. Při vyšetřování průběhu funkce určujeme:

• definiční obor a obor hodnot
• průsečíky grafu funkce se souřadnými osami
  • Průsečík grafu funkce s osou $y$ řešením rovnice $f(0)=y$
  • Průsečík grafu funkce s osou $x$ řešením rovnice $f(x)=0$
• intervaly spojitosti funkce
  • body nespojitosti
  • limity v bodech nespojitosti
• první derivaci funkce a její pomocí určíme
  • intervaly monotonie
  • stacionární body resp. lokální extrémy
• druhou derivaci a její pomocí určíme
  • intervaly konvexnosti a konkávnosti
  • inflexní body
• rovnice asymptot
• funkční hodnoty ve stacionárních a inflexních bodech.

Stacionární (červené) a inflexní (modré) body funkce $x+\sin x$

Jako stacionární bod resp. inflexní bod funkce $f$ se označuje každý bod $a$ jejího definičního oboru, v němž je první resp. druhá derivace funkce nulová, tj. ve stacionárním resp. inflexním bodě platí: $f^{\prime }(a)=0$ resp. $f^{″}(a)=0$ pokud v tomto bodě derivace existují.

Jako extremální bod funkce $f$ se označuje každý stacionární bod $a$ jejího definičního oboru, v němž je druhá derivace funkce kladná (ostré lokální minimum) resp. záporná (ostré lokální maximum), tj. v extremálním bodě platí: $f^{″}(a)>0$ resp. $f^{″}(a)<0$ pokud v tomto bodě derivace existují.

Příklad

Průběh funkce $x\ln x$

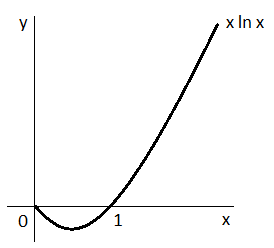
Vyšetřujme průběh funkce $y=x\ln x$:

• zatímco lineární funkce $y=x$ je definována pro všechna $x$, funkce logaritmus je definována pouze pro $x>0$, tj. definičním oborem vyšetřované funkce bude interval $(0,+\mathrm{\infty })$.

• průsečík s osou $y$ získáme z rovnice $y=0\ln 0$, tj. $y=0$ a průsečík s osou $x$ získáme z rovnice $x\ln x=0$, tj. $x_1=0$ a $x_2=1$.

• určíme limitu v každém bodě $a$ definičního oboru: $\underset{x\to a}{\lim }x\ln x=a\ln a$, tj. funkce je na definičním oboru spojitá.

• určíme první derivaci funkce a položíme ji rovnu nule: $y^{\prime }=\ln x+1=0$, tj. $\ln x=-1$, tj. bod $x=\frac{1}{e}$ je stacionární a

funkce je rostoucí na intervalu, ve kterém platí $y^{\prime }>0$, tj. $\ln x>-1$, tj. pro $x>\frac{1}{e}$,

funkce je klesající na intervalu, ve kterém platí $y^{\prime }<0$, tj. $\ln x<-1$, tj. pro $x<\frac{1}{e}$,

tj. z rozložení intervalů monotonie lze určit, že stacionární bod je ostré lokální minimum ($y^{\prime \prime }(\frac{1}{e})=e>0$), funkce je tedy zdola omezená.

• vzhledem k tomu, že $y^{\prime \prime }=\frac{1}{x}>0$ na celém definičním oboru, nemá funkce žádný inflexní bod.

• asymptoty k funkci neexistují, neboť $\underset{x\to +\mathrm{\infty }}{\lim }\frac{f(x)}{x}=\underset{x\to +\mathrm{\infty }}{\lim }\ln x=+\mathrm{\infty }$.

• funkční hodnota lokálního minima je $y(\frac{1}{e})=-\frac{1}{e}$.

• určíme-li v nulovém bodě pomocí l'Hospitalova pravidla jednostrannou limitu zprava: $\underset{x\to 0+}{\lim }x\ln x=\underset{x\to 0+}{\lim }\frac{\ln x}{\frac{1}{x}}=\underset{x\to 0+}{\lim }\frac{\frac{1}{x}}{-\frac{1}{x^2}}=0$, funkci můžeme v nulovém bodě dodefinovat: $y(0)=0$, tj. rozšířit definiční obor na interval $⟨0,+\mathrm{\infty })$.

Prostá funkce

Prostá funkce je v matematice funkce, která žádnou funkční hodnotu nenabývá vícekrát než jednou. Je to důležitá vlastnost spojená s řešením rovnic, protože nás informuje o tom, že rovnice mající na jedné straně prostou funkci a na druhé straně její funkční hodnotu nemá více než jedno řešení. Tuto informaci je důležité mít například před použitím numerických metod řešení rovnic.

Definice

Funkci $f$ na definičním oboru $D$ označujeme jako prostou na $D$, pokud pro každé dvě hodnoty $x_1\ne x_2$ z $D$ platí $f(x_1)\ne f(x_2)$, tedy pro libovolnou dvojici různých hodnot $x$ jsou různé i hodnoty funkce $f(x)$.

Příklad

Příkladem prosté funkce je lineární funkce $f(x)=ax+b$ pro $a\ne 0$, naopak příkladem neprosté funkce je kvadratická funkce $f(x)=x^2$, neboť např. $f(-2)=f(2)=4$.

Vlastnosti

Pokud je funkce $f$ na $D$ ryze monotonní (tedy její hodnoty neustále rostou nebo neustále klesají), pak je na $D$ také prostá, neboť se v žádném jiném bodě nemůže vrátit do stejného výsledku. Opačné tvrzení (tedy že pokud je funkce prostá, pak je i ryze monotonní) platí pouze pro spojité funkce, u nichž nemůže dojít ke "skokovým" změnám funkčních hodnot; pro tyto funkce jsou tak tvrzení o prostosti a ryzí monotonicitě ekvivalentní.

Mezi funkcemi nespojitými však existují případy prostých funkcí, které ryze monotonní nejsou. Např. prostá funkce $1\to 3,2\to 4,3\to 2,4\to 1$ je na množině $\{1,2\}$ rostoucí, zatímco na množině $\{3,4\}$ klesající, a na svém celém definičním oboru tedy není monotonní.

Souvislost s inverzní funkcí

K prosté funkci existuje funkce inverzní – např. k funkci exponenciální je inverzní funkcí logaritmus. Funkcím, které nejsou prosté, nelze inverzní funkci přiřadit; pokud jsou však prosté na určité podmnožině svého definičního oboru, lze je invertovat na této podmnožině – takto je např. druhá odmocnina inverzní funkcí k druhé mocnině na intervalu $⟨0,\mathrm{\infty })$, protože druhá mocnina je na tomto intervalu prostá.

Omezená funkce

Červená funkce (Hyperbola) je omezená pouze zdola, zelená (Parabola) pouze shora a modrá (Hyperbolický tangens) je omezená shora i zdola

Mějme funkci $f(x)$ a množinu $A\subseteq D(f)$.

Existuje-li číslo $K$ takové, že pro všechna $x\in A$ platí $f(x)\le K$, pak říkáme, že funkce $f$ je na $D(f)$ shora ohraničená (omezená). Existuje-li supremum oboru hodnot funkce $f$, pak také existuje číslo $K$, a funkce je tedy shora omezená.

Existuje-li číslo $L$ takové, že pro všechna $x\in A$ platí $f(x)\ge L$, pak říkáme, že funkce $f$ je na $D(f)$ zdola ohraničená (omezená). Existuje-li infimum oboru hodnot funkce $f$, pak také existuje číslo $L$, a funkce je tedy zdola omezená.

Existuje-li číslo $M$ takové, že pro všechna $x\in A$ platí $|f(x)|\le M$, pak říkáme, že funkce $f$ je na $D(f)$ ohraničená (omezená). Funkce omezená je tedy omezená shora i zdola, přičemž $M=\max \{|K|,|L|\}$.

Obor hodnot omezené funkce má konečné infimum i supremum. Pokud funkce není omezená zdola ani shora, pak je neohraničená (neomezená).

Algebraická funkce

Polynomiální funkce

Polynomiální funkci lze vyjádřit ve tvaru:

$f(x)=P_n(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n$,

kde $a_n\ne 0$ a $n$ je stupeň polynomu $P$.

Racionální funkce

Racionální funkci lze vyjádřit ve tvaru:

$f(x)=\frac{P_n(x)}{Q_m(x)}=\frac{a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n}{b_0+b_{1}x+b_2{x}^2+\cdots +b_m{x}^m}$,

kde $b_m\ne 0$ a $m$ je stupeň polynomu $Q$.

Iracionální funkce

Iracionální funkce jsou funkce obsahující ve svém předpisu výraz $x^{\frac{n}{m}}$, kde $n$ a $m$ jsou vzájemně nesoudělná čísla, jako např. druhá odmocnina.

Transcendentní funkce

Funkce, které nejsou algebraické, se označují jako transcendentní. Mezi nižší transcendentní funkce se řadí funkce goniometrické, cyklometrické, hyperbolické, hyperbolometrické či exponenciální a logaritmické. Mezi vyšší transcendentní funkce se řadí například chybová funkce či eliptické integrály.

Mnohoznačná funkce

Termín mnohoznačná (vícehodnotová) funkce vznikl v komplexní analýze analytickým rozšířením jednoznačné (jednohodnotové) funkce. Často se stává, že známe hodnotu komplexní analytické funkce $f(z)$ komplexní proměnné $z$ v určitém okolí bodu $z=a$. To je případ funkcí definovaných implicitně nebo Taylorovou řadou v okolí $z=a$. V takovém případě lze rozšířit obor hodnot jednohodnotové funkce $f(z)$ podél křivek v komplexní rovině vedoucích z bodu $z=a$ do bodu $z=b$. Přitom zjistíme, že hodnota rozšířené funkce v bodě $z=b$ závisí na zvolené křivce z $a$ do $b$ a protože žádná z nových hodnot není přirozenější než ostatní, jsou všechny začleněny do vícehodnotové funkce. Příkladem je n-tá odmocnina komplexního čísla, což je n-značná funkce, např. pro druhou odmocninu dostaneme:

$f(z)=\sqrt{z}=\sqrt{|z|}{e}^{i\frac{\phi }{2}}=\sqrt{|z|}(\cos \frac{\phi }{2}+i\sin \frac{\phi }{2})=\{\begin{array}{cc}\sqrt{|z|},& \text{pro }\phi =0\\ i\sqrt{|z|},& \text{pro }\phi =\pi \end{array}$

Operace s funkcemi

Mějme funkci $f(x)$ resp. $g(x)$ s definičním oborem $D_f$ resp. $D_g$. Společný definiční obor obou funkcí je průnikem obou definičních oborů, tj. $D=D_f\cap D_g$.

Binární operace

Součtem funkcí $f,g$ na $D$ označíme funkci $h$ takovou, že $h(x)=f(x)+g(x)$ pro všechna $x\in D$.

Součinem funkcí $f,g$ na $D$ označíme funkci $h$ takovou, že $h(x)=f(x)\cdot g(x)$ pro všechna $x\in D$.

Podílem funkcí $f,g$ na $D^{\prime }$ označíme funkci $h$ takovou, že $h(x)=\frac{f(x)}{g(x)}$ pro všechna $x\in D^{\prime }$, kde $D^{\prime }$ = $D-\{x\in D_g|g(x)=0\}$.

Skládáním funkcí $f,g$ na $D^{\prime }$ označíme funkci $h$ takovou, že $h(x)=(f\circ g)(x)=f(g(x))$ pro všechna $x\in D^{\prime }$, kde $D^{\prime }$ = $\{x\in D_g|g(x)\in D_f\}$.

Konvolucí funkcí $f,g$ na $D$ označíme funkci $h$ takovou, že $h(x)=(f*g)(x)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(\alpha )g(x-\alpha )\mathrm{d}\alpha$ pro všechna $x\in D$.

Korelací funkcí $f,g$ na $D$ označíme funkci $h$ takovou, že $h(x)=(f\star g)(x)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{f}^{*}(\alpha )g(x+\alpha )\mathrm{d}\alpha =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{f}^{*}(\alpha -x)g(\alpha )\mathrm{d}\alpha$ pro všechna $x\in D$.

Složením funkcí $f$ a $g$ je množina $f\circ g=\{[x,y]|\mathrm{\exists }[x,z]\in g\wedge [z,y]\in f\}$.

Operace skládání funkcí nemusí být v obecném případě komutativní. Zatímco konvoluce je funkcí komutativní, pro vzájemnou korelaci to obecně neplatí (je komutativní pouze pro Hermitovské funkce, tj. funkce, pro které platí $f^{*}(x)=f(-x)$ pro všechna $x\in D$, kde symbol ${*}^{}$ značí komplexní sdružení).

Unární operace

Inverzí funkce $f$ na $V_f$ označíme funkci $f^{-1}$ takovou, že $f^{-1}(y)=x$, kde pro každé $y\in V_f$ existuje právě jedno $x\in D_f$ tak, že $y=f(x)$, tj. $f$ je prostá funkce.

Graf inverzní funkce $f^{-1}$ je osově souměrný s grafem funkce $f$ podle osy 1. a 3. kvadrantu. Z toho plyne, že identická funkce $f(x)=x$ je inverzní sama k sobě.

Literatura

• Šablona:Citace monografie

Související články

• Definiční obor
• Obor hodnot
• Limita funkce
• Spojitá funkce
• Konvexní funkce
• Konkávní funkce
• Monotónní funkce
• Sudé a liché funkce
• Periodická funkce
• Harmonická funkce
• Komplexní funkce

Externí odkazy

• Šablona:Commonscat
• Šablona:Wikislovník
• functions.wolfram.com – online encyklopedie vzorců a grafických ztvárnění funkcí
• Vykreslování grafů funkcí (i jejich derivací a integrálů)