Gama funkce

Gama funkce (někdy také označovaná jako Eulerův integrál druhého druhu) je zobecněním faktoriálu pro obor komplexních čísel. Používá se v mnoha oblastech matematiky, např. pro popis některých rozdělení pravděpodobnosti.
Funkce je značena pomocí řeckého písmene gama a je definována jako holomorfní rozšíření integrálu:
Ačkoliv integrál samotný konverguje jen, je-li reálná část z kladná, gama funkce je definována pro libovolné komplexní číslo, kromě nekladných celých čísel.
Vlastnosti
Funkce je spojitá pro . Funkce diverguje pro celá . Tyto body jsou póly prvního řádu a odpovídající rezidua jsou . Jiné singularity nemá a jedná se tedy o funkci meromorfní v celém oboru .
Pro n-tou derivaci platí vztah
- .
V oblasti kladných reálných čísel má gama funkce minimum v bodě .
Užitečné vztahy
- Pro přirozená čísla platí
- Pro kladná polocelá čísla můžeme psát pomocí dvojného faktoriálu
Některé hodnoty
nedefinováno nedefinováno nedefinováno
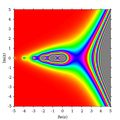
Grafy
-
Reálná část Γ(z)
-
Imaginární část Γ(z)
-
Absolutní hodnota Γ(z)
-
Absolutní hodnota Γ(z), 3D pohled