Vlastní vektory a vlastní čísla

Vlastní vektor lineárního operátoru je nenulový vektor, jehož směr se uplatněním operátoru nemění; může se měnit jeho velikost a orientace, což lze interpretovat jako násobení nenulovým skalárem. Tento skalár se nazývá vlastní číslo (též vlastní hodnota nebo charakteristické číslo) přidružené či příslušné uvažovanému vlastnímu vektoru. Geometricky se transformace vlastního vektoru operátorem projeví zvětšením/zmenšením vektoru buď bez změny orientace (kladné vlastní číslo) nebo s obrácením orientace (záporné vlastní číslo). Množina vlastních vektorů, které náleží stejnému vlastnímu číslu, se nazývá vlastní prostor operátoru přidružený k danému vlastnímu číslu.
Vlastní vektor může mít v konkrétních aplikacích i jiná označení, je například zvykem říkat vlastní řešení (pokud je vektor řešením nějaké rovnice), vlastní funkce (pokud jde o funkci), vlastní stav (pokud vektor popisuje kvantový stav) apod.
Vlastní čísla a vlastní vektory hrají důležitou roli nejen v lineární algebře, ale i funkcionální analýze, kybernetice nebo v kvantové fyzice.
Definice a značení
Vlastní vektor lineárního operátoru je takový nenulový vektor , pro který existuje číslo tak, že platí:
- .
Číslo se nazývá vlastní číslo (též charakteristické číslo) operátoru a vlastní vektor operátoru příslušný vlastní hodnotě .
V kvantové mechanice se často lze setkat se zápisem anebo kde označuje operátor a příslušné vlastní číslo. Operátor je často diferenciální operátor na nějakém prostoru funkcí nebo distribucí.
Výpočet vlastních čísel a vlastních vektorů matice
Nechť je zadaná reálná nebo komplexní čtvercová matice , je sloupcový vektor délky a je reálné nebo komplexní číslo. Rovnice , jejíž levou stranu chápeme jako násobení matice vektorem a pravou stranu jako násobení skaláru vektorem, obsahuje známou matici a neznámé veličiny a . Tato maticová rovnice se dá přepsat jako soustava lineárních rovnic
pro .
Proměnnou na pravé straně lze pomocí Kroneckerova delta vyjádřit jako
Dosazením do předchozího vztahu pak dostaneme
- ,
což lze vyjádřit maticově jako
- ,
kde je jednotková matice. Na tento vztah lze nahlížet jako na homogenní soustavu lineárních algebraických rovnic o neznámých. Ta má netriviální (nenulové) řešení právě tehdy, když je matice soustavy singulární, tzn. platí
- ,
což lze rozepsat
- .
Tato rovnice se nazývá charakteristická rovnice. Rovnice podobného typu bývají také označovány jako sekulární rovnice, protože dříve sloužily k výpočtům pohybů planet (jejich odchylek od eliptických drah).
Polynom na levé straně této rovnice se nazývá charakteristický polynom matice a jeho kořeny jsou vlastními čísly matice . Proto má matice vždy vlastních čísel, z nichž se některá mohou opakovat. Počet opakování, tj. násobnost kořene charakteristického polynomu nazýváme algebraickou násobností vlastního čísla.
Vlastní vektory matice vyhovují rovnici pro jednotlivá vlastní čísla.
Libovolný nenulový násobek vlastního vektoru je rovněž vlastním vektorem, není však považován za jiný vlastní vektor. Ke kořenu charakteristického polynomu násobnosti existuje nejvýše vzájemně lineárně nezávislých vlastních vektorů. Počet lineárně nezávislých vlastních vektorů odpovídajících vlastnímu číslu , tj. , kde značí jádro matice, se nazývá geometrická násobnost vlastního čísla.
Vztah mezi algebraickou a geometrickou násobností lze snadno nahlédnout pomocí Jordanova rozkladu matice.
Příklad
Určete vlastní čísla a vlastní vektory matice
Charakteristická rovnice má tvar
- .
Po jejím rozepsání (tedy jednoduše vyčíslíme determinant a položíme jej roven nule) dostaneme kvadratickou rovnici
Řešením této rovnice získáme vlastní čísla
Vlastní vektor příslušný vlastní hodnotě získáme řešením soustavy lineárních rovnic
Řešením této rovnice je např. vektor
Vlastní vektor příslušný vlastní hodnotě získáme řešením soustavy lineárních rovnic
Řešením této rovnice je např. vektor
Vlastnosti
- Nula je vlastním číslem matice právě tehdy, když je matice singulární. Je-li matice regulární, pak nula není jejím vlastním číslem.
- Je-li matice symetrická a reálná (tj. obsahuje pouze reálná čísla), pak všechna její vlastní čísla jsou reálná.
- Jestliže k matici existuje inverzní matice , pak je vlastním číslem matice tehdy, je-li vlastním číslem matice . Přitom platí, že vlastní vektory matice odpovídající vlastnímu číslu jsou stejné jako vlastní vektory matice odpovídající vlastnímu číslu .
- Pokud má matice vlastní číslo a odpovídající vlastní vektor , pak matice má vlastní číslo a jemu odpovídající vlastní vektor je .
- Je-li vlastním číslem reálné matice komplexní číslo , pak je také komplexně sdružené číslo vlastním číslem matice .
- Je-li lineární operátor hermitovský, jsou všechna vlastní čísla reálná.
Spektrum operátoru
Jako spektrum omezeného lineárního operátoru se označuje množina komplexních čísel , pro které není operátor invertovatelný. Množina všech vlastních čísel tvoří část spektra operátoru. Tato část se nazývá bodové (diskrétní) spektrum. V případě konečnorozměrných operátorů (čtvercových matic konečných rozměrů) je celé spektrum bodové. U nekonečněrozměrných operátorů mohou existovat i další části spektra, které nejsou bodové.
Pokud ke každému vlastnímu číslu přísluší právě jedna vlastní funkce , pak říkáme, že operátor má prosté (nedegenerované) spektrum.
Pokud některým vlastním číslům přísluší několik lineárně nezávislých vlastní funkcí , tzn.
- ,
kde , pak hovoříme o degenerovaném spektru. Počet lineárně nezávislých funkcí se nazývá násobností (stupněm) degenerace.
Aplikace
Vlastní hodnoty geometrických zobrazení
Následující tabulka obsahuje příklady transformací v rovině s jejich 2×2 maticemi, vlastními hodnotami a vlastními vektory.
| Zvětšení | Různé zvětšení ve směru os x a y | Rotace | Horizontální zkosení | Hyperbolická rotace | |
|---|---|---|---|---|---|
| Ilustrace | 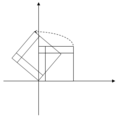
|
||||
| Matice | |||||
| Charakteristický polynom |
|||||
| Vlastní hodnoty, | |||||
| Algebraická násobnost, |
|||||
| Geometrická násobnost, |
|||||
| Vlastní vektory | Všechny nenulové vektory |
Charakteristická rovnice rotace je kvadratická rovnice s diskriminantem . Je-li Šablona:Mvar celočíselný násobek 180° je vlastní číslo +1 nebo -1. Jinak je diskriminant záporný, a obě vlastní čísla nejsou reálná, ale komplexní ; všechny vlastní vektory pak mají složky, které nejsou reálnými čísly, protože kromě uvedených speciálních případů rotace mění směr každého nenulového vektoru v rovině.
Lineární transformace, která převádí čtverec na obdélník stejné plochy (Šablona:Vjazyce2) má jedno vlastní číslo rovné převrácené hodnotě druhého.
Schrödingerova rovnice

Příkladem rovnice s vlastními čísly, kde transformace je reprezentována diferenciálním operátorem, je časově nezávislá Schrödingerova rovnice v kvantové mechanice:
kde Hamiltonián je diferenciální operátor druhého řádu a vlnová funkce je jednou z jeho vlastních funkcí odpovídajících vlastnímu číslu interpretovanému jako energie.
V případě, kdy nás zajímají pouze řešení pro vázané stavy Schrödingerovy rovnice, jak je tomu často v kvantové chemii, budeme hledat v prostoru kvadraticky integrovatelných funkcí. Protože tento prostor je Hilbertův prostor s dobře definovaným skalárním součinem, můžeme zavést bázi, v níž lze reprezentovat jednorozměrným polem (tj. vektorem) a maticí. To nám umožňuje reprezentovat Schrödingerovu rovnici v maticovém tvaru.
Pro zápis se často používá Diracova notace. Vektor, který reprezentuje stav systému v Hilbertově prostoru kvadraticky integrovatelných funkcí, je reprezentován . S použitím této notace lze Schrödingerovu rovnici zapsat takto:
kde je vlastní stav (který někteří autoři značí ) a reprezentuje vlastní číslo. je pozorovatelný samoadjungovaný operátor, nekonečněrozměrná obdoba Hermitovské matice. Stejně jako v maticovém případě chápeme ve výše uvedené rovnici jako vektor získaný aplikací transformace na .
Odkazy
Reference
Literatura
- Šablona:Citace monografie
- Šablona:Citace monografie
- Šablona:Citace elektronické monografie
- Šablona:Citace elektronické monografie