Rozdělení beta

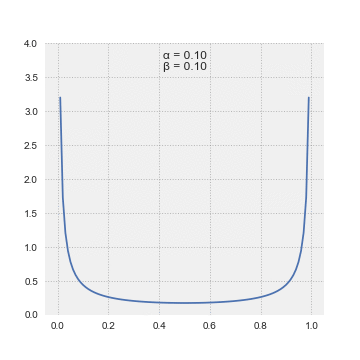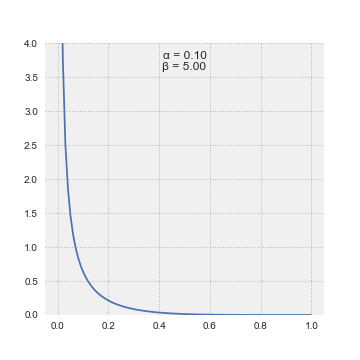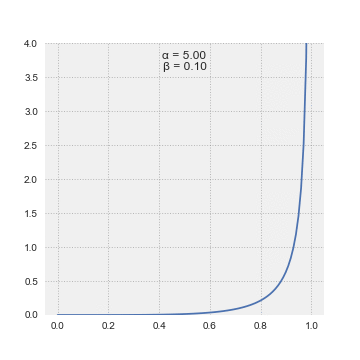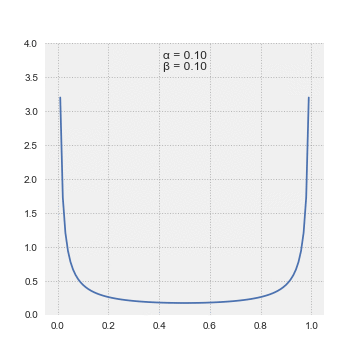
Rozdělení beta pro různé hodnoty parametrů

Rozdělení beta je rodina spojitých rozdělení pravděpodobnosti definovaných na intervalu [0, 1]. Nejčastěji se parametrizuje dvěma kladnými parametry označenými α a β, popřípadě někdy p a q,které se objevují jako exponenty náhodné proměnné a řídí tvar distribuce. Zobecnění na více proměnných se nazývá Dirichletovo rozdělení.

Rozdělení beta se široce používá k modelování chování náhodných proměnných omezených na intervaly konečné délky. V bayesovské statistice je distribuce beta konjugovaný prior pro modelování jevů s Bernoulliho, binomickým, inverzním binomickým a geometrickým rozdělením. Distribuce beta je vhodný model pro náhodné chování procent a podílů.

Hustota pravděpodobnosti (pdf) pro Šablona:Nowrap a tvarové parametry α, β > 0 je mocninná funkce proměnné x a její reflexe Šablona:Nowrap:

$\begin{array}{cc}f(x;\alpha ,\beta )& =\mathrm{k}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{a}\cdot x^{\alpha -1}(1-x{)}^{\beta -1}\\ & =\frac{x^{\alpha -1}(1-x{)}^{\beta -1}}{\underset{0}{\overset{1}{\int }}{u}^{\alpha -1}(1-u{)}^{\beta -1}du}\\ & =\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{x}^{\alpha -1}(1-x{)}^{\beta -1}\\ & =\frac{1}{\mathrm{B}(\alpha ,\beta )}{x}^{\alpha -1}(1-x{)}^{\beta -1}\end{array}$

kde Γ(z) je gama funkce. Beta funkce, $\mathrm{B}$ (po které má rozdělení své jméno, jelikož jeho pdf má matematicky podobný tvar jako tato funkce), je normalizační konstanta zajišťující, že celková pravděpodobnost je 1.

Střední hodnota a rozptyl náhodné proměnné X s rozdělením beta jsou:

$\mathrm{E}[X]=\frac{\alpha }{\alpha +\beta }$

$\mathrm{V}\mathrm{a}\mathrm{r}[X]=\frac{\alpha \beta }{(\alpha +\beta +1)(\alpha +\beta {)}^2}$.

Externí odkazy

• Šablona:Commonscat