Dvojbran

Obr. 1: Příklad dvojbranu s definicemi symbolů. Aby se jednalo o dvojbran, musí být splněny bránové podmínky: Vstupní a výstupní napětí musí být rozdílem příslušných uzlových napětí; proudy protékající oběma póly jedné brány musí být stejně velké, ale opačného znaménka.Šablona:Sfn

Dvojbran (Šablona:Vjazyce2), případně čtyřpól, je v elektronice elektrický obvod nebo zařízení se dvěma páry svorek pro připojení k vnějším obvodům. Na svorkách je zkoumáno chování obvodu (proud a napětí - vnější veličiny). Vnitřní zapojení může být jakkoliv složité. Typické využití dvojbranů je u transformátorů, děličů napětí, elektronických filtrů a zesilovačů.

Dvojice svorek tvoří bránu, pokud proudy jimi tekoucí vyhovují nutným podmínkám známým jako bránové podmínky: oběma svorkami jedná brány teče stejný proud opačného směru. Brány tvoří rozhraní, kterými se dvojbran propojuje s jinými obvody, jediné body, kam se přivádí signál nebo odkud se signál odebírá. Bránu 1 zpravidla považujeme za vstupní a bránu 2 za výstupní.

Dvojbrany se používají v matematické obvodové analýze.

Rozdělení

Pasivní filtr (dolní propust) zapojený jako dvojbran

T zapojení

Podle fyzikální struktury

• lineární (pouze lineární součástky)
• nelineární (obsahuje i nelineární prvky, jako operační zesilovače a tranzistory)
• aktivní (s vnějším zdrojem)
• pasivní (pouze RLC součástky)

Podle topologie

Podle zapojení:

• T článek
• Π článek
• Γ článek
• složitější články (X, přemostěný T, XTX, …)

Podle symetrie:

• podélně symetrický
• příčně symetrický
• nesymetrický

Aplikace

Dvojbranový model se používá v technikách matematické obvodové analýzy pro rozdělení větších obvodů na části. Dvojbran je považován za „černou skříňku“, jejíž vlastnosti jsou zadány maticí čísel. Díky tomu lze snadno spočítat jeho odezvu na signály přivedené na brány, bez řešení všech interních napětí a proudů v obvodu. To umožňuje snadno porovnávat podobné obvody nebo zařízení. Za dvojbrany jsou často považovány například tranzistory, které jsou charakterizovány Šablona:Mvar-parametry (viz níže) udávanými výrobci. Libovolný lineární obvod se čtyřmi svorkami lze považovat za dvojbran, pokud neobsahuje nezávislý zdroj a vyhovuje bránové podmínce.

Příklady obvodů, které lze analyzovat jako dvojbrany, jsou filtry, přizpůsobovací obvody, přenosová vedení, transformátory, a modely malých signálů pro tranzistory (např. hybridní-pí model). Analýza pasivního dvojbranového obvodu je přímým důsledkem věty o reciprocitě, kterou jako první odvodil Lorentz.

V dvojbranových matematických modelech je dvojbran popsán čtvercovou maticí 2×2 komplexních čísel. Běžně používané modely jsou Šablona:Mvar-parametry, Šablona:Mvar-parametry, Šablona:Mvar-parametry, Šablona:Mvar-parametry, a Šablona:Mvar-parametry, které jsou podrobně popsány níže. Tyto jsou vesměs omezeny na lineární obvody, protože podkladovým předpokladem jejich odvození je, že libovolná daná obvodová podmínka je lineární superpozicí různých podmínek pro obvody nakrátko a naprázdno. Obvykle se zapisují v maticové notaci, a vyjadřují vztahy mezi proměnnými

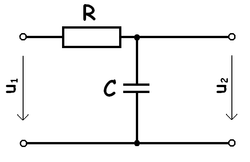
Šablona:Math – napětí na bráně 1

Šablona:Math – proud do brány 1

Šablona:Math – napětí na bráně 2

Šablona:Math – proud do brány 2

které jsou uvedeny na obrázku 1. Rozdíly mezi různými modely spočívají v tom, které z těchto proměnných jsou považovány za nezávislé. Tyto proudové a napěťové proměnné jsou nejužitečnější při nízkých nebo středních frekvencích. Při vysokých frekvencích (například pro mikrovlnné frekvence) je vhodnější použít proměnné pro výkon a energii, a dvojbranový přístup proud–napětí nahradit přístupem podle rozptylových parametrů.

Obecné vlastnosti

V praxi se často objevují určité vlastnosti dvojbranů, jejichž použití značné zjednoduší analýzu. Patří k nim:

Reciproké obvody

Řekneme, že obvod je reciproký, pokud napětí, které se objeví na bráně 2, vyvolané proudem přivedeným na bránu 1 je stejné jako napětí, které se objeví na bráně 1, když je stejný proud přiveden na bránu 2. Vzájemná zaměnitelnost napětí a proudů dává ekvivalentní definici reciprocity. Obvod, který se skládá pouze z lineárních pasivních součástek (tj. rezistorů, kondenzátorů a cívek) je obvykle reciproký, významnou výjimkou jsou pasivní cirkulátory a izolátory, které obsahují zmagnetizované materiály. Reciproké obecně nejsou obvody obsahující aktivní součástky např. generátory nebo tranzistory.

Symetrické obvody

Obvod je symetrický, pokud jeho vstupní impedance je rovna jeho výstupní impedanci. Symetrické obvody jsou obvykle, i když ne nutně, také fyzicky symetrické. Někdy nás zajímají také antisymetrické obvody. Jde o obvody, jejichž vstupní a výstupní impedance jsou vzájemně duální.

Bezztrátové obvody

Bezztrátový obvod je takový, který neobsahuje rezistory nebo jiné prvky, na nichž vzniká výkonová ztráta.

Impedanční parametry (z-parametry)

Obr. 2: Z-ekvivalent dvojbranu s nezávislými proměnnými Šablona:Math a Šablona:Math. Přestože na obrázku jsou rezistory mohou být použity obecné impedance.

$\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)=\left(\begin{array}{cc}{z}_{11}& z_{12}\\ z_{21}& z_{22}\end{array}\right)\left(\begin{array}{c}{I}_1\\ I_2\end{array}\right)$

kde

$\begin{array}{cccc}{z}_{11}& \stackrel{\text{def}}{=}{\frac{V_1}{I_1}|}_{I_2=0}& z_{12}& \stackrel{\text{def}}{=}{\frac{V_1}{I_2}|}_{I_1=0}\\ z_{21}& \stackrel{\text{def}}{=}{\frac{V_2}{I_1}|}_{I_2=0}& z_{22}& \stackrel{\text{def}}{=}{\frac{V_2}{I_2}|}_{I_1=0}\end{array}$

Všechny Šablona:Mvar-parametry mají rozměr Ohmu.

Pro reciproké obvody platí Šablona:Math; pro symetrické obvody Šablona:Math; pro reciproké bezztrátové obvody jsou všechny parametry Šablona:Math čistě imaginární.

Příklad: bipolární proudové zrcadlo s emitorovou degenerací

Obr. 3: Bipolární proudové zrcadlo: Šablona:Math je referenční proud a Šablona:Math je výstupní proud; psaní veličin malými písmeny indikuje, že jde o celkové proudy, které zahrnují i stejnosměrnou složku.

Obr. 4: Bipolární proudové zrcadlo pro malý signál: Šablona:Math je amplituda dostatečně malého referenčního proudu a Šablona:Math je amplituda dostatečně malého výstupního proudu.

Obrázek 3 ukazuje bipolární proudové zrcadlo s emitorovými rezistory pro zvýšení výstupního odporu. Tranzistor Šablona:Math je diodově propojený, což znamená, že jeho napětí kolektor-báze je nulové. Obrázek 4 ukazuje obvod, který je pro malé signály ekvivalentní s Obrázek 3. Tranzistor Šablona:Math je reprezentován svým emitorovým odporem Šablona:Math:

$r_{\mathrm{E}}\approx \frac{\text{termální napětí, }{V}_{\mathrm{T}}}{\text{proud emitoru, }{I}_E},$

zjednodušení je možné, protože závislý proudový zdroj v hybridním-pi modelu pro Šablona:Math odebírá stejný proud jako rezistor Šablona:Math připojený přes Šablona:Math. Druhý tranzistor Šablona:Math je reprezentován svým hybridním-pi modelem. Tabulka 1 níže ukazuje výrazy z-parametrů, díky nimž je z-ekvivalentní obvod z Obrázku 2 elektricky ekvivalentní s obvodem s malým signálem z Obrázku 4.

Tabulka 1

	Výraz	Aproximace
$R_{21}={\frac{V_2}{I_1}|}_{I_2=0}$	$-(\beta r_{\mathrm{O}}-R_{\mathrm{E}})\frac{r_{\mathrm{E}}+R_{\mathrm{E}}}{r_{\pi }+r_{\mathrm{E}}+2R_{\mathrm{E}}}$	$-\beta r_{\mathrm{o}}\frac{r_{\mathrm{E}}+R_{\mathrm{E}}}{r_{\pi }+2R_{\mathrm{E}}}$
$R_{11}={\frac{V_1}{I_1}|}_{I_2=0}$	$(r_{\mathrm{E}}+R_{\mathrm{E}})\Vert (r_{\pi }+R_{\mathrm{E}})$
$R_{22}={\frac{V_2}{I_2}|}_{I_1=0}$	$(1+\beta \frac{R_{\mathrm{E}}}{r_{\pi }+r_{\mathrm{E}}+2R_{\mathrm{E}}})r_{\mathrm{O}}+\frac{r_{\pi }+r_{\mathrm{E}}+R_{\mathrm{E}}}{r_{\pi }+r_{\mathrm{E}}+2R_{\mathrm{E}}}{R}_{\mathrm{E}}$	$(1+\beta \frac{R_{\mathrm{E}}}{r_{\pi }+2R_{\mathrm{E}}})r_{\mathrm{O}}$
$R_{12}={\frac{V_1}{I_2}|}_{I_1=0}$	$R_{\mathrm{E}}\frac{r_{\mathrm{E}}+R_{\mathrm{E}}}{r_{\pi }+r_{\mathrm{E}}+2R_{\mathrm{E}}}$	$R_{\mathrm{E}}\frac{r_{\mathrm{E}}+R_{\mathrm{E}}}{r_{\pi }+2R_{\mathrm{E}}}$

V těchto parametrech je vidět záporná zpětná vazba zavedená rezistory Šablona:Math. Pokud se používají například jako aktivní zátěž v diferenciálním zesilovači, Šablona:Math, což činí výstupní impedance zrcadla přibližně

$R_{22}-R_{21}\approx \frac{2\beta r_{\mathrm{O}}{R}_{\mathrm{E}}}{r_{\pi }+2R_{\mathrm{E}}}$

v porovnání s pouze Šablona:Math bez zpětné vazby (to je s Šablona:Math = 0 Ω). Impedance na referenční straně zrcadla, přibližně

$R_{11}-R_{12}\approx \frac{r_{\pi }}{r_{\pi }+2R_{\mathrm{E}}}(r_{\mathrm{E}}+R_{\mathrm{E}}),$

je zároveň pouze malá hodnota, která je však stále větší než Šablona:Math bez zpětné vazby. Pozitivní je, že velký výstupní odpor v aplikacích diferenciálního zesilovače zvyšuje zisk v rozdílovém režimu, a malý vstupní odpor zrcadla je žádoucí, aby se zabránilo Millerově efektu.

Admitanční parametry (y-parametry)

Obr. 5: Y-ekvivalent dvojbran s nezávislými proměnnými Šablona:Math a Šablona:Math. Přestože na obrázku jsou rezistory, mohou být použity obecné impedance.

$\left(\begin{array}{c}{I}_1\\ I_2\end{array}\right)=\left(\begin{array}{cc}{y}_{11}& y_{12}\\ y_{21}& y_{22}\end{array}\right)\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)$

kde

$\begin{array}{cccc}{y}_{11}& \stackrel{\text{def}}{=}{\frac{I_1}{V_1}|}_{V_2=0}& y_{12}& \stackrel{\text{def}}{=}{\frac{I_1}{V_2}|}_{V_1=0}\\ y_{21}& \stackrel{\text{def}}{=}{\frac{I_2}{V_1}|}_{V_2=0}& y_{22}& \stackrel{\text{def}}{=}{\frac{I_2}{V_2}|}_{V_1=0}\end{array}$

Všechny Y-parametry mají rozměr Siemens.

Pro reciproké obvody platí Šablona:Math; pro symetrické obvody Šablona:Math; pro reciproké bezztrátové obvody jsou všechny Šablona:Math čistě imaginární.

Hybridní parametry (h-parametry) Šablona:Kotva

Šablona:Math a Šablona:Math; Je použita převrácená hodnota parametru Šablona:Math jako by se jednalo o rezistor.

$\left(\begin{array}{c}{V}_1\\ I_2\end{array}\right)=\left(\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{22}\end{array}\right)\left(\begin{array}{c}{I}_1\\ V_2\end{array}\right)$

kde

$\begin{array}{cccc}{h}_{11}& \stackrel{\text{def}}{=}{\frac{V_1}{I_1}|}_{V_2=0}& h_{12}& \stackrel{\text{def}}{=}{\frac{V_1}{V_2}|}_{I_1=0}\\ h_{21}& \stackrel{\text{def}}{=}{\frac{I_2}{I_1}|}_{V_2=0}& h_{22}& \stackrel{\text{def}}{=}{\frac{I_2}{V_2}|}_{I_1=0}\end{array}$

Tento model se často volí, když je na výstupu požadován proudový zesilovač. Je nejpoužívanějším modelem pro popis tranzistoru v nízkofrekvenčních obvodech. Ve schématu uvedené rezistory mohou být obecnými impedancemi.

Šablona:Mvar-parametry mimo hlavní diagonálu jsou bezrozměrné veličiny, zatímco členy na hlavní diagonále mají vzájemně reciproký rozměr.

• Šablona:Math je vstupní impedance
• Šablona:Math je zpětný napěťový přenos (zpětné zesílení)
• Šablona:Math je proudový zesilovací činitel
• Šablona:Math je výstupní vodivost

Pro reciproké obvody platí Šablona:Math; pro symetrické obvody Šablona:Math; pro reciproké bezztrátové obvody jsou Šablona:Math a Šablona:Math reálné, zatímco Šablona:Math a Šablona:Math jsou čistě imaginární.

Příklad: zesilovač se společnou bází

Obr. 7: Zesilovač se společnou bází se zdrojem střídavého proudu Šablona:Math jako vstupem signálu a nespecifikovanou zátěží dodávající napětí Šablona:Math a závislý proud Šablona:Math

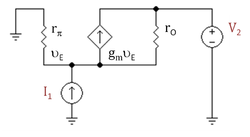
Poznámka: Vzorce v Tabulce 2 zajišťují, že Šablona:Mvar-ekvivalentní obvod tranzistoru z Obrázku 6 souhlasí s jeho hybridním pí modelem pro malé signály a nízké frekvence na obrázku 7. Notace: Šablona:Math je bázový odpor tranzistoru, Šablona:Math je výstupní odpor, a Šablona:Math je vzájemná transkonduktance. Záporné znaménko pro Šablona:Math odráží konvence, že Šablona:Math jsou kladný, když orientovaný do dvojbran. Nenulová hodnota pro Šablona:Math znamená, že výstupní napětí způsobuje vstupní napětí, to jest, tento zesilovač je obousměrný. Pokud Šablona:Math, zesilovač je jednosměrný.

Tabulka 2

	Výraz	Aproximace
$h_{21}={\frac{I_2}{I_1}|}_{V_2=0}$	$-\frac{\frac{\beta }{\beta +1}{r}_{\mathrm{O}}+r_{\pi }}{r_{\mathrm{O}}+r_{\pi }}$	$-\frac{\beta }{\beta +1}$
$h_{11}={\frac{V_1}{I_1}|}_{V_2=0}$	$r_{\pi }\Vert r_{\mathrm{O}}$	$r_{\pi }$
$h_{22}={\frac{I_2}{V_2}|}_{I_1=0}$	$\frac{1}{(\beta +1)(r_{\mathrm{O}}+r_{\pi })}$	$\frac{1}{(\beta +1)r_{\mathrm{O}}}$
$h_{12}={\frac{V_1}{V_2}|}_{I_1=0}$	$\frac{r_{\pi }}{r_{\mathrm{O}}+r_{\pi }}$	$\frac{r_{\pi }}{r_{\mathrm{O}}}\ll 1$

Historie

Šablona:Mvar-parametrům se zpočátku říkalo sériovo-paralelní parametry. Termín hybridní pro popis těchto parametrů poprvé použil D. A. Alsberg v roce 1953 v „Tranzistor metrology“. V roce 1954 sdružený výbor IRE a AIEE přijal termín Šablona:Mvar-parametry a doporučil, aby se tyto parametry staly standardní metodou pro testování a udávání charakteristik tranzistorů, protože byly „překvapivě přizpůsobitelné fyzickým charakteristikám tranzistorů“. V roce 1956 se doporučení stalo vydaným standardem; 56 IRE 28.S2. Po sloučení těchto dvou organizací do IEEE se standard stal Std 218-1956 a byl znovu potvrzen v roce 1980, ale nyní byl opuštěn.

Inverzní hybridní parametry (g-parametry) Šablona:Kotva

Obr. 8: G-ekvivalentní dvojport znázorňující nezávislé veličiny Šablona:Matha Šablona:Math; je použita převrácená hodnota parametru Šablona:Math jako by se jednalo o rezistor.

$\left(\begin{array}{c}{I}_1\\ V_2\end{array}\right)=\left(\begin{array}{cc}{g}_{11}& g_{12}\\ g_{21}& g_{22}\end{array}\right)\left(\begin{array}{c}{V}_1\\ I_2\end{array}\right)$

kde

$\begin{array}{cccc}{g}_{11}& \stackrel{\text{def}}{=}{\frac{I_1}{V_1}|}_{I_2=0}& g_{12}& \stackrel{\text{def}}{=}{\frac{I_1}{I_2}|}_{V_1=0}\\ g_{21}& \stackrel{\text{def}}{=}{\frac{V_2}{V_1}|}_{I_2=0}& g_{22}& \stackrel{\text{def}}{=}{\frac{V_2}{I_2}|}_{V_1=0}\end{array}$

Tento obvod se často používá, pokud na výstupu požadujeme napěťový zesilovač. g-parametry mimo diagonálu jsou bezrozměrné, zatímco diagonální členy mají rozměry vzájemně reciproké. Místo rezistorů uvedených ve schématu mohou být obecné impedance.

Příklad: zesilovač se společnou bází

Obr. 9: Zesilovač se společnou bází se zdrojem střídavého napětí Šablona:Math jako vstupem signálu a nespecifikovanou zátěží dodávající proud Šablona:Math při závislém napětí Šablona:Math.

Poznámka: Tabelované vzorce v Tabulce 3 zajišťují, že Šablona:Mvar-ekvivalentní obvod tranzistoru z Obrázek 8 souhlasí s jeho hybridním pí modelem pro malé signály a nízké frekvence na obrázku 9. Notace: Šablona:Math je bázový odpor tranzistoru, Šablona:Math je výstupní odpor, a Šablona:Math je vzájemná transkonduktance. Záporné znaménko pro Šablona:Math odráží konvenci, že proudy Šablona:Math jsou kladné, pokud jsou orientované do dvojbranu. Nenulová hodnota Šablona:Math znamená, že výstupní proud způsobuje vstupní proud, to jest, že tento zesilovač je dvoustranný. Pokud Šablona:Math, zesilovač je jednostranný.

Tabulka 3

	Výraz	Aproximace
$g_{21}={\frac{V_2}{V_1}|}_{I_2=0}$	$\frac{r_{\mathrm{o}}}{r_{\pi }}+g_{\mathrm{m}}{r}_{\mathrm{O}}+1$	$g_{\mathrm{m}}{r}_{\mathrm{O}}$
$g_{11}={\frac{I_1}{V_1}|}_{I_2=0}$	$\frac{1}{r_{\pi }}$	$\frac{1}{r_{\pi }}$
$g_{22}={\frac{V_2}{I_2}|}_{V_1=0}$	$r_{\mathrm{O}}$	$r_{\mathrm{O}}$
$g_{12}={\frac{I_1}{I_2}|}_{V_1=0}$	$-\frac{\beta +1}{\beta }$	$-1$

ABCD-parametry Šablona:Kotva

Šablona:Mvar-parametry se nazývají řetězové, kaskádové nebo přenosové parametry. Existují různé definice Šablona:Mvar parametrů, nejobvyklejší je,

$\left(\begin{array}{c}{V}_1\\ I_1\end{array}\right)=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)\left(\begin{array}{c}{V}_2\\ -I_2\end{array}\right)$

Poznámka: Někteří autoři používají opačný směr I₂ a proto před tímto členem nemají záporné znaménko.

kde

$\begin{array}{cccc}A& \stackrel{\text{def}}{=}{\frac{V_1}{V_2}|}_{I_2=0}& B& \stackrel{\text{def}}{=}{-\frac{V_1}{I_2}|}_{V_2=0}\\ C& \stackrel{\text{def}}{=}{\frac{I_1}{V_2}|}_{I_2=0}& D& \stackrel{\text{def}}{=}{-\frac{I_1}{I_2}|}_{V_2=0}\end{array}$

Pro reciproké obvody platí Šablona:Math; pro symetrické obvody Šablona:Math; pro obvody který jsou reciproké a bezztrátové, jsou hodnoty Šablona:Mvar a Šablona:Mvar čistě reálné, zatímco Šablona:Mvar a Šablona:Mvar jsou čistě imaginární.

Výhodou této reprezentace je, že když se parametry používají pro reprezentaci kaskády dvojbranů, matice se píšou ve stejném pořadí, v jakém se kreslí schéma zapojení, to jest zleva doprava. Používají se však i jiné definice.

$\left(\begin{array}{c}{V}_2\\ -I_2\end{array}\right)=\left(\begin{array}{cc}{A}^{\prime }& B^{\prime }\\ C^{\prime }& D^{\prime }\end{array}\right)\left(\begin{array}{c}{V}_1\\ I_1\end{array}\right)$

kde

$\begin{array}{cccc}{A}^{\prime }& \stackrel{\text{def}}{=}{\frac{V_2}{V_1}|}_{I_1=0}& B^{\prime }& \stackrel{\text{def}}{=}{\frac{V_2}{I_1}|}_{V_1=0}\\ C^{\prime }& \stackrel{\text{def}}{=}{-\frac{I_2}{V_1}|}_{I_1=0}& D^{\prime }& \stackrel{\text{def}}{=}{-\frac{I_2}{I_1}|}_{V_1=0}\end{array}$

Záporné znaménko u Šablona:Math je použito, aby výstupní proud jedné kaskádované fáze (jak se objevuje v matici) byl rovný vstupnímu proudu následující. Bez záporného znaménka by tyto proudy měly opačný smysl, protože podle konvence proud, který teče do brány, má kladný směr. Díky tomu lze vstupní maticový vektor napětí a proudů přímo nahradit maticovou rovnicí předchozí kaskádované fáze pro vytvoření kombinované matice Šablona:Mvar.

Někteří autoři reprezentují parametry Šablona:Mvar maticí prvků označených Šablona:Math a inverzní parametry Šablona:Mvar maticí prvků označených Šablona:Math pro zkrácení zápisu a zamezení záměně parametrů s obvodovými prvky.

$\begin{array}{cc}\left[𝐚\right]& =\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)\\ \left[𝐛\right]& =\left(\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right)=\left(\begin{array}{cc}{A}^{\prime }& B^{\prime }\\ C^{\prime }& D^{\prime }\end{array}\right)\end{array}$

Tabulka přenosových parametrů

Následující tabulka ukazuje parametry Šablona:Mvar a inverzní parametry Šablona:Mvar některých jednoduchých obvodových prvků.

Prvek	Šablona:Math matice	Šablona:Math matice	Poznámky
sériová impedance	$\left(\begin{array}{cc}1& Z\\ 0& 1\end{array}\right)$	$\left(\begin{array}{cc}1& -Z\\ 0& 1\end{array}\right)$	Šablona:Mvar je impedance
bočníková admitance	$\left(\begin{array}{cc}1& 0\\ Y& 1\end{array}\right)$	$\left(\begin{array}{cc}1& 0\\ -Y& 1\end{array}\right)$	Šablona:Mvar je admitance
sériová indukčnost	$\left(\begin{array}{cc}1& sL\\ 0& 1\end{array}\right)$	$\left(\begin{array}{cc}1& -sL\\ 0& 1\end{array}\right)$	Šablona:Mvar je induktance Šablona:Mvar je komplexní úhlová frekvence
bočníková indukčnost	$\left(\begin{array}{cc}1& 0\\ \frac{1}{sL}& 1\end{array}\right)$	$\left(\begin{array}{cc}1& 0\\ -\frac{1}{sL}& 1\end{array}\right)$	Šablona:Mvar je induktance Šablona:Mvar je komplexní úhlová frekvence
sériová kapacita	$\left(\begin{array}{cc}1& \frac{1}{sC}\\ 0& 1\end{array}\right)$	$\left(\begin{array}{cc}1& -\frac{1}{sC}\\ 0& 1\end{array}\right)$	Šablona:Mvar je kapacita Šablona:Mvar je komplexní úhlová frekvence
bočníková kapacita	$\left(\begin{array}{cc}1& 0\\ sC& 1\end{array}\right)$	$\left(\begin{array}{cc}1& 0\\ -sC& 1\end{array}\right)$	Šablona:Mvar je kapacita Šablona:Mvar je komplexní úhlová frekvence
přenosové vedení	$\left(\begin{array}{cc}\cosh (\gamma l)& Z_0\sinh (\gamma l)\\ \frac{1}{Z_0}\sinh (\gamma l)& \cosh (\gamma l)\end{array}\right)$	$\left(\begin{array}{cc}\cosh (\gamma l)& -Z_0\sinh (\gamma l)\\ -\frac{1}{Z_0}\sinh \left(\gamma l\right)& \cosh (\gamma l)\end{array}\right)$	Šablona:Math je charakteristická impedance Šablona:Mvar je konstanta šíření ($\gamma =\alpha +i\beta$) Šablona:Mvar je délka přenosového vedení (Šablona:Mvar)

Rozptylové parametry (S-parametry)

Obr. 17: Vlnová terminologie použitá pro definici Šablona:Mvar-parametru.

Předchozí parametry jsou vesměs definovány pomocí napětí a proudů bran. Šablona:Mvar-parametry jsou odlišné, a jsou definovaný pomocí incident a odražených vln branami. Šablona:Mvar-parametry se používají primárně pro UHF a mikrovlnné frekvence, kde je obtížné měřit napětí a proudy přímo. Na druhou stranu, incident a odražený výkon lze snadno měřit použitím směrových vazebných členů. Definice je,

$\left(\begin{array}{c}{b}_1\\ b_2\end{array}\right)=\left(\begin{array}{cc}{S}_{11}& S_{12}\\ S_{21}& S_{22}\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\end{array}\right)$

kde Šablona:Mvar jsou incident vlny a Šablona:Mvar jsou odražený vlny na bráně Šablona:Mvar. Je obvyklý definovat Šablona:Mvar a Šablona:Mvar pomocí druhá odmocnina výkonu. Následně, existuje vztah s vlna napětí (viz hlavní článek pro detaily).

Pro reciproké obvody platí Šablona:Math; pro symetrické obvody Šablona:Math; pro antisymetrické obvody Šablona:Math; pro bezztrátové reciproké obvody $|S_{11}|=|S_{22}|$ a $|S_{11}{|}^2+|S_{12}{|}^2=1.$

Rozptylové přenosové parametry (T-parametry)

Šablona:Viz též Rozptylové přenosové parametry jsou stejně jako rozptylové parametry definovány pomocí incident a odražený vlny. Rozdílem je, že Šablona:Mvar-parametry se týkají vln na bráně 1 do vlny na bráně 2 zatímco Šablona:Mvar-parametry se týkají odražených vln do incident vlny. V tomto ohledu Šablona:Mvar-parametry vyplnit stejný roli jako Šablona:Mvar parametry a umožňuje Šablona:Mvar-parametry kaskádovaných sítí být spočítaný znásobením matic komponent obvody. Šablona:Mvar-parametry můžeme stejně jako jako Šablona:Mvar parametry nazývat přenosovými parametry. Definice je,

$\left(\begin{array}{c}{a}_1\\ b_1\end{array}\right)=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right)\left(\begin{array}{c}{b}_2\\ a_2\end{array}\right)$

Šablona:Mvar-parametry nelze přímo měřit tak snadno jako Šablona:Mvar-parametry. Šablona:Mvar-parametry však lze snadno zkonvertovat na Šablona:Mvar-parametry, jak je popsáno v hlavním článku.

Kombinace dvojbranových sítí

Při propojení dvou nebo více dvojbranových obvodů lze dvojbranové parametry kombinovaného obvodu nalézt provedením určitých maticových operací s maticemi parametrů jednotlivých dvojbranů. Maticové operace mohou být obzvlášť jednoduché při vhodné volbě dvojbranových parametrů podle způsobu propojení dvojbranů. Například při sériovém propojení bran jsou nejlepší Šablona:Mvar-parametry.

Kombinační pravidla je třeba používat s rozmyslem. Některá propojení (když se propojují různé potenciály) vedou k porušení bránových podmínek, a kombinační pravidlo již nebude platit. Pro kontrolu přípustnosti kombinace lze použít Bruneho test. Tento problém lze překonat umístěním ideálních transformátorů 1:1 na výstupy problematických dvojbranů. Tím se nezmění parametry dvojbranů, ale zajistí se, že při propojení nedojde k porušení bránová podmínek. Příklad tohoto problému je ukázán na sériovo-sériovém propojení na obrazcích 11 a 12 níže.

Sériovo-sériové propojení

Obr. 10: Dva dvojbranové obvody se vstupními i výstupními branami zapojenými sériově.

Pokud jsou dvojbrany propojeny sériovo-sériově, jak je ukázáno na obrázku 10, nejlepší volbou dvojbranových parametrů jsou Šablona:Mvar-parametry. Šablona:Mvar-parametry kombinovaného obvodu je možné nalézt sečtením matic Šablona:Mvar-parametrů.

$[𝐳]=[𝐳{]}_1+[𝐳{]}_2$

Obr. 11: Příklad nesprávného propojení dvojbranů. Šablona:Math sponího dvojbranu je zkratován.

Obr. 12: Použití ideálních transformátorů pro obnovení bránové podmínky pro propojené obvody.

Jak bylo zmíněno výše, některé obvody této analýze přímo neodpovídají. Jednoduchý příkladem je dvojbran sestávající z Šablona:Mvar-obvodu rezistorů Šablona:Math a Šablona:Math. Šablona:Mvar-parametry tohoto obvodu jsou:

$[𝐳{]}_1=\left(\begin{array}{cc}{R}_1+R_2& R_2\\ R_2& R_2\end{array}\right)$

Obrázek 11 ukazuje dva takové identické obvody propojené sériovo-sériově. Celkové Šablona:Mvar-parametry dané sečtením matic jsou

$[𝐳]=[𝐳{]}_1+[𝐳{]}_2=2[𝐳{]}_1=\left(\begin{array}{cc}2R_1+2R_2& 2R_2\\ 2R_2& 2R_2\end{array}\right)$

Přímá analýza kombinovaného obvodu však ukazuje, že

$[𝐳]=\left(\begin{array}{cc}{R}_1+2R_2& 2R_2\\ 2R_2& 2R_2\end{array}\right)$

Nesoulad lze vysvětlit tím, že Šablona:Math dolního dvojbranu je obcházen zkratem mezi dvěma svorkami výstupních bran. Dostáváme ne proud tekoucí jednou svorkou v každý ze vstupních bran ze dvou jednotlivých obvodů. V důsledku toho je bránová podmínka porušena pro obě vstupní brány původního obvodu, protože proud stále může téct druhou svorkou. Tento problém lze vyřešit vložením ideálního transformátoru do výstupní brány alespoň jednoho z dvojbranů. Přestože se jedná o běžný učebnicový přístup k prezentaci teorie dvojbranů, o použití transformátorů je třeba v praxi rozhodnout pro každý jednotlivý návrh.

Paralelně-paralelní propojení

Obr. 13: Dva dvojbranové obvody se vstupními branami zapojenými paralelně výstupními branami zapojenými paralelně.

Při paralelně-paralelním propojení dvojbranů znázorněným na obrázku 13 jsou nejlepší volbou dvojbranových parametrů Šablona:Mvar-parametry. Šablona:Mvar-parametry kombinovaného obvodu lze získat maticovým sčítáním matic Šablona:Mvar-parametrů.

$[𝐲]=[𝐲{]}_1+[𝐲{]}_2$

Sériovo-paralelní propojení

Obr. 14: Dva dvojbranové obvody se vstupními branami zapojenými sériové zapojení výstupními branami zapojenými paralelně.

Pokud jsou dvojbrany propojeny sériovo-paralelně, jak je ukázáno na obrázku 14, nejlepší volbou dvojbranových parametrů jsou Šablona:Mvar-parametry. Šablona:Mvar-parametry kombinovaného obvodu lze získat maticovým sečtením matic Šablona:Mvar-parametrů.

$[𝐡]=[𝐡{]}_1+[𝐡{]}_2$

Paralelně-sériové propojení

Obr. 15: Dva dvojbranové obvody se vstupními branami propojenými paralelně a výstupními branami propojenými sériově.

Pokud jsou dvojbrany propojeny paralelně-sériově, jak je ukázáno na obrázku 15, nejlepší volbou dvojbranových parametrů jsou Šablona:Mvar-parametry. Šablona:Mvar-parametry kombinovaného obvodu lze získat maticovým sečtením matic Šablona:Mvar-parametrů.

$[𝐠]=[𝐠{]}_1+[𝐠{]}_2$

Kaskádové propojení

Obr. 16: Dva dvojbranové obvody s výstupní branou prvního zapojený do vstupní branou druhého.

Pokud jsou dvojbrany propojený s výstupní branou prvního zapojenou na vstupní bránu druhého (kaskádové propojení) jak je ukázáno na obrázku 16, nejlepší volba dvojbranový parametry je Šablona:Mvar-parametry. Šablona:Mvar-parametry kombinovaného obvodu lze získat násobením jejich matic ze dvou jednotlivou Šablona:Mvar-parametr matice.

$[𝐚]=[𝐚{]}_1\cdot [𝐚{]}_2$

Řetěz Šablona:Mvar dvojbranů lze vyjádřit maticovým násobením Šablona:Mvar matic. Pro zkombinování kaskády Šablona:Mvar-parametrových matic, je třeba je opět znásobit, ale v opačném pořadí, tady;

$[𝐛]=[𝐛{]}_2\cdot [𝐛{]}_1$

Příklad

Předpokládejme, že máme dvojbran sestávající ze sériového rezistoru Šablona:Mvar následovaného bočníkovým kondenzátorem Šablona:Mvar. Celý obvod můžeme modelovat jako kaskádu dvou jednodušších obvodů:

$\begin{array}{cc}[][𝐛{]}_1& =\left(\begin{array}{cc}1& -R\\ 0& 1\end{array}\right)\\ [𝐛{]}_2& =\left(\begin{array}{cc}1& 0\\ -sC& 1\end{array}\right)\end{array}$

Přenosová matice celého obvodu Šablona:Math je jednoduše maticovým násobením přenosové matice obou obvodových prvků:

$\begin{array}{cc}[][𝐛]& =[𝐛{]}_2\cdot [𝐛{]}_1\\ & =\left(\begin{array}{cc}1& 0\\ -sC& 1\end{array}\right)\left(\begin{array}{cc}1& -R\\ 0& 1\end{array}\right)\\ & =\left(\begin{array}{cc}1& -R\\ -sC& 1+sCR\end{array}\right)\end{array}$

Tedy:

$\left(\begin{array}{c}{V}_2\\ -I_2\end{array}\right)=\left(\begin{array}{cc}1& -R\\ -sC& 1+sCR\end{array}\right)\left(\begin{array}{c}{V}_1\\ I_1\end{array}\right)$

Vztahy mezi parametry

	Šablona:Math	Šablona:Math	Šablona:Math	Šablona:Math	Šablona:Math	Šablona:Math
Šablona:Math	$\left(\begin{array}{cc}{z}_{11}& z_{12}\\ z_{21}& z_{22}\end{array}\right)$	$\frac{1}{\mathrm{\Delta }\mathbf{[}𝐲\mathbf{]}}\left(\begin{array}{cc}{y}_{22}& -y_{12}\\ -y_{21}& y_{11}\end{array}\right)$	$\frac{1}{h_{22}}\left(\begin{array}{cc}\mathrm{\Delta }\mathbf{[}𝐡\mathbf{]}& h_{12}\\ -h_{21}& 1\end{array}\right)$	$\frac{1}{g_{11}}\left(\begin{array}{cc}1& -g_{12}\\ g_{21}& \mathrm{\Delta }\mathbf{[}𝐠\mathbf{]}\end{array}\right)$	$\frac{1}{a_{21}}\left(\begin{array}{cc}{a}_{11}& \mathrm{\Delta }\mathbf{[}𝐚\mathbf{]}\\ 1& a_{22}\end{array}\right)$	$\frac{1}{b_{21}}\left(\begin{array}{cc}-b_{22}& -1\\ -\mathrm{\Delta }\mathbf{[}𝐛\mathbf{]}& -b_{11}\end{array}\right)$
Šablona:Math	$\frac{1}{\mathrm{\Delta }\mathbf{[}𝐳\mathbf{]}}\left(\begin{array}{cc}{z}_{22}& -z_{12}\\ -z_{21}& z_{11}\end{array}\right)$	$\left(\begin{array}{cc}{y}_{11}& y_{12}\\ y_{21}& y_{22}\end{array}\right)$	$\frac{1}{h_{11}}\left(\begin{array}{cc}1& -h_{12}\\ h_{21}& \mathrm{\Delta }\mathbf{[}𝐡\mathbf{]}\end{array}\right)$	$\frac{1}{g_{22}}\left(\begin{array}{cc}\mathrm{\Delta }\mathbf{[}𝐠\mathbf{]}& g_{12}\\ -g_{21}& 1\end{array}\right)$	$\frac{1}{a_{12}}\left(\begin{array}{cc}{a}_{22}& -\mathrm{\Delta }\mathbf{[}𝐚\mathbf{]}\\ -1& a_{11}\end{array}\right)$	$\frac{1}{b_{12}}\left(\begin{array}{cc}-b_{11}& 1\\ \mathrm{\Delta }\mathbf{[}𝐛\mathbf{]}& -b_{22}\end{array}\right)$
Šablona:Math	$\frac{1}{z_{22}}\left(\begin{array}{cc}\mathrm{\Delta }\mathbf{[}𝐳\mathbf{]}& z_{12}\\ -z_{21}& 1\end{array}\right)$	$\frac{1}{y_{11}}\left(\begin{array}{cc}1& -y_{12}\\ y_{21}& \mathrm{\Delta }\mathbf{[}𝐲\mathbf{]}\end{array}\right)$	$\left(\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{22}\end{array}\right)$	$\frac{1}{\mathrm{\Delta }\mathbf{[}𝐠\mathbf{]}}\left(\begin{array}{cc}{g}_{22}& -g_{12}\\ -g_{21}& g_{11}\end{array}\right)$	$\frac{1}{a_{22}}\left(\begin{array}{cc}{a}_{12}& \mathrm{\Delta }\mathbf{[}𝐚\mathbf{]}\\ -1& a_{21}\end{array}\right)$	$\frac{1}{b_{11}}\left(\begin{array}{cc}-b_{12}& 1\\ -\mathrm{\Delta }\mathbf{[}𝐛\mathbf{]}& -b_{21}\end{array}\right)$
Šablona:Math	$\frac{1}{z_{11}}\left(\begin{array}{cc}1& -z_{12}\\ z_{21}& \mathrm{\Delta }\mathbf{[}𝐳\mathbf{]}\end{array}\right)$	$\frac{1}{y_{22}}\left(\begin{array}{cc}\mathrm{\Delta }\mathbf{[}𝐲\mathbf{]}& y_{12}\\ -y_{21}& 1\end{array}\right)$	$\frac{1}{\mathrm{\Delta }\mathbf{[}𝐡\mathbf{]}}\left(\begin{array}{cc}{h}_{22}& -h_{12}\\ -h_{21}& h_{11}\end{array}\right)$	$\left(\begin{array}{cc}{g}_{11}& g_{12}\\ g_{21}& g_{22}\end{array}\right)$	$\frac{1}{a_{11}}\left(\begin{array}{cc}{a}_{21}& -\mathrm{\Delta }\mathbf{[}𝐚\mathbf{]}\\ 1& a_{12}\end{array}\right)$	$\frac{1}{b_{22}}\left(\begin{array}{cc}-b_{21}& -1\\ \mathrm{\Delta }\mathbf{[}𝐛\mathbf{]}& -b_{12}\end{array}\right)$
Šablona:Math	$\frac{1}{z_{21}}\left(\begin{array}{cc}{z}_{11}& \mathrm{\Delta }\mathbf{[}𝐳\mathbf{]}\\ 1& z_{22}\end{array}\right)$	$\frac{1}{y_{21}}\left(\begin{array}{cc}-y_{22}& -1\\ -\mathrm{\Delta }\mathbf{[}𝐲\mathbf{]}& -y_{11}\end{array}\right)$	$\frac{1}{h_{21}}\left(\begin{array}{cc}-\mathrm{\Delta }\mathbf{[}𝐡\mathbf{]}& -h_{11}\\ -h_{22}& -1\end{array}\right)$	$\frac{1}{g_{21}}\left(\begin{array}{cc}1& g_{22}\\ g_{11}& \mathrm{\Delta }\mathbf{[}𝐠\mathbf{]}\end{array}\right)$	$\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)$	$\frac{1}{\mathrm{\Delta }\mathbf{[}𝐛\mathbf{]}}\left(\begin{array}{cc}{b}_{22}& -b_{12}\\ -b_{21}& b_{11}\end{array}\right)$
Šablona:Math	$\frac{1}{z_{12}}\left(\begin{array}{cc}{z}_{22}& -\mathrm{\Delta }\mathbf{[}𝐳\mathbf{]}\\ -1& z_{11}\end{array}\right)$	$\frac{1}{y_{12}}\left(\begin{array}{cc}-y_{11}& 1\\ \mathrm{\Delta }\mathbf{[}𝐲\mathbf{]}& -y_{22}\end{array}\right)$	$\frac{1}{h_{12}}\left(\begin{array}{cc}1& -h_{11}\\ -h_{22}& \mathrm{\Delta }\mathbf{[}𝐡\mathbf{]}\end{array}\right)$	$\frac{1}{g_{12}}\left(\begin{array}{cc}-\mathrm{\Delta }\mathbf{[}𝐠\mathbf{]}& g_{22}\\ g_{11}& -1\end{array}\right)$	$\frac{1}{\mathrm{\Delta }\mathbf{[}𝐚\mathbf{]}}\left(\begin{array}{cc}{a}_{22}& -a_{12}\\ -a_{21}& a_{11}\end{array}\right)$	$\left(\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right)$

Kde Šablona:Math je Determinant matice Šablona:Math.

Určité dvojice matic mají obzvláště jednoduchý vztah. Admitanční parametry tvoří inverzní matici impedančních parametrů, inverzní hybridní parametry jsou inverzní maticí hybridních parametrů, a Šablona:Math tvar Šablona:Mvar-parametrů je inverzní matice k Šablona:Math forma. Tj.

$\begin{array}{cc}\left[𝐲\right]& =[𝐳{]}^{-1}\\ \left[𝐠\right]& =[𝐡{]}^{-1}\\ \left[𝐛\right]& =[𝐚{]}^{-1}\end{array}$

Šablona:KotvaObvody s více než dvěma branami

Zatímco dvojbranné obvody jsou velmi běžné (například zesilovače a filtry), jiné elektrické obvody např. směrové vazebné členy a cirkulátory mají více než 2 brány. Následující reprezentace jsou použitelné pro obvody s libovolným počtem bran:

• [[Admitanční parametry|Admitanční (Šablona:Mvar) parametry]]
• [[Impedanční parametry|Impedanční (Šablona:Mvar) parametry]]
• [[Rozptylové parametry|Rozptylové (Šablona:Mvar) parametry]]

Například trojportové impedanční parametry vedou k následujícímu vztahu:

$\left(\begin{array}{c}{V}_1\\ V_2\\ V_3\end{array}\right)=\left(\begin{array}{ccc}{Z}_{11}& Z_{12}& Z_{13}\\ Z_{21}& Z_{22}& Z_{23}\\ Z_{31}& Z_{32}& Z_{33}\end{array}\right)\left(\begin{array}{c}{I}_1\\ I_2\\ I_3\end{array}\right)$

Následující reprezentace jsou však nutně omezeny na dvojbrany:

• Hybridní (Šablona:Mvar) parametry
• Inverzní hybridní (Šablona:Mvar) parametry
• Přenosové (Šablona:Mvar) parametry
• Rozptylové přenosové (Šablona:Mvar) parametry

Přechod dvojbranu na jednobran

Dvojbran má čtyři proměnné, z nichž dvě jsou nezávislé. Pokud je jedna z bran ukončená zátěží neobsahující nezávislý zdroj, pak si tato zátěž vynucuje vztah mezi napětím a proudem této brány. Tím se ztratí jeden stupeň volnosti, takže obvod bude mít pouze jeden nezávislý parametr. Dvojbran tak přejde na jednobranovou impedanci vůči zbývající nezávislé proměnné.

Uvažujme například impedanční parametry

$\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)=\left(\begin{array}{cc}{z}_{11}& z_{12}\\ z_{21}& z_{22}\end{array}\right)\left(\begin{array}{c}{I}_1\\ I_2\end{array}\right)$

Připojení zátěže Šablona:Math na bránu 2 efektivně přidá omezení

$V_2=-Z_{\mathrm{L}}{I}_2$

Záporné znaménko je způsobeno tím, že kladný směr Šablona:Math je orientován do dvojbranu místo do zátěže. Rozšířená rovnice přejde na tvar

$\begin{array}{cc}{V}_1& =Z_{11}{I}_1+Z_{12}{I}_2\\ -Z_{\mathrm{L}}{I}_2& =Z_{21}{I}_1+Z_{22}{I}_2\end{array}$

Druhou rovnici lze snadno vyřešit pro Šablona:Math jako funkci proudu Šablona:Math a tento výraz je možné dosadit za Šablona:Math do první rovnice ponechává Šablona:Math ( a Šablona:Math a Šablona:Math ) jako funkce Šablona:Math

$\begin{array}{cc}{I}_2& =-\frac{Z_{21}}{Z_{\mathrm{L}}+Z_{22}}{I}_1\\ V_1& =Z_{11}{I}_1-\frac{Z_{12}{Z}_{21}}{Z_{\mathrm{L}}+Z_{22}}{I}_1\\ & =(Z_{11}-\frac{Z_{12}{Z}_{21}}{Z_{\mathrm{L}}+Z_{22}})I_1=Z_{\text{in}}{I}_1\end{array}$

Ve výsledku tedy Šablona:Math zaznamená (vidí) vstupní impedance Šablona:Math a vliv dvojbranu na vstupní obvod byl efektivně stažen na jednobran; tj. na jednoduchou impedanci se dvěma svorkami.

Odkazy

Literatura

• Šablona:Citace elektronické monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie
• Šablona:Citace monografie

Historie h-parametrů

• Šablona:Citace monografie
  • také publikováno jako “Transistor metrology“, Transactions of the IRE Professional Group on Electron Devices, vol. ED-1, iss. 3, pp. 12–17, Srpen 1954.
• AIEE-IRE sdružené výbor, "Proposed methods of testing transistors", Transactions of the American Institute of Electrical Engineers: Communications and Electronics, pp. 725–740, Leden 1955.
• "IRE Standards on solid-state devices: methods of testing transistors, 1956", Proceedings of IRE, vol. 44, iss. 11, pp. 1542–1561, listopad, 1956.
• IEEE Standard Methods of Testing Transistors, IEEE Std 218-1956.

Související články

• Admitanční parametry
• Impedanční parametry
• Rozptylové parametry
• Elektronický filtr
• Zesilovač
• Dělič napětí
• Transformátor

Externí odkazy

• Šablona:Commonscat