Biangulární souřadnice

Šablona:Upravit Biangulární souřadnice jsou soustava souřadnic v rovině určená úsečkou, kde poloha bodu je určena dvěma úhly. Tento typ souřadnic jako první zkoumal Lazare Nicholas Marguerite Carnot, který své výsledky publikoval v roce 1803.

Poloha bodu

V rovině je dána úsečka $\overline{AB}$. Pak poloha každého bodu $C$ v této rovině (s výjimkou bodů ležících na přímce $\overline{AB}$) je jednoznačně dána úhly $\mathrm{\angle }CAB$ a $\mathrm{\angle }CBA$.

Polohu bodů na přímce $\overline{AB}$ nelze určit, jelikož úhly $\mathrm{\angle }CAB$ a $\mathrm{\angle }CBA$ pro různé body jsou stejné - nulové nebo přímé (180°).

Zaměření bodu v biangulárních souřadnicích

Máme bod, zvaný $C$, v rovině a chceme jej vyjádřit v této soustavě.

Definice bodu c úhlovými souřadnicemi α a β v rovině.

Zvolme v rovině úsečku $AB$, jejíž délka je jednotková. Oba krajní body této úsečky spojme s bodem $C$.

Najdeme úhly $\alpha$ a $\beta$, odpovídajíci úhlům $CAB$ a $CBA$ v tomto pořadí.

Úsečka $AB$ a úhly $\alpha$ a $\beta$ tak určují polohu bodu v nové soustavě souřadnic a úhly $\alpha$ a $\beta$ jsou těmito souřadnicemi.

Převod na souřadnice kartézské

$x=\frac{c\mathrm{t}\mathrm{g}\beta }{\mathrm{t}\mathrm{g}\alpha +\mathrm{tg}\beta }$

$y=\frac{c\mathrm{t}\mathrm{g}\alpha \mathrm{t}\mathrm{g}\beta }{\mathrm{t}\mathrm{g}\alpha +\mathrm{t}\mathrm{g}\beta }$

a pro zpětný převod souřadnic x-y na α - β použijeme rovnice:

$\alpha =\mathrm{arctg2}\left(\frac{y}{x}\right),$

$\beta =\mathrm{arctg2}\left(\frac{y}{c-x}\right),$

kde arctg2 je zobecnění funkce arkus tangens často užívané při inverzích vztahů v rovině.

Rovnice kuželoseček v úhlových souřadnicích

Šablona:Neověřeno část V úhlových souřadnicích se dá jednoduše vyjádřit rovnice jistých kuželoseček v rovině.

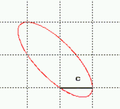
Rovnice elipsy: $\mathrm{t}\mathrm{g}\beta =\frac{1}{\mathrm{t}\mathrm{g}\alpha }+1,5$

Rovnice paraboly: $\mathrm{t}\mathrm{g}\beta =\frac{1}{\mathrm{t}\mathrm{g}\alpha }+2$

Rovnice hyperboly: $\mathrm{t}\mathrm{g}\beta =\frac{1}{\mathrm{t}\mathrm{g}\alpha }+3$

• 
  Elipsa, definovaná úhlovými souřadnicemi v rovině
• 
  Parabola, definovaná úhlovými souřadnicemi v rovině
• 
  Hyperbola, definovaná úhlovými souřadnicemi v rovině