Průběh funkce

Průběh funkce

Pokud se snažíme zjistit alespoň přibližný tvar grafu funkce, hovoříme o tom, že vyšetřujeme průběh funkce. Při tom se zkoumají různé vlastnosti funkce a hledají se funkční body, které graf funkce dělí na intervaly mající příslušnou vlastnost. Při vyšetřování průběhu funkce se zajímáme o následující vlastnosti:

• definiční obor a obor hodnot
• určíme periodičnost, sudost a lichost funkce a její ohraničenost
• průsečíky grafu se souřadnými osami
  • Průsečík grafu funkce $f(x)$ s osou $y$ získáme dosazením hodnoty $x=0$ do funkce $f$, tzn. získáme hodnotu $y_0=f(0)$.
  • Průsečík grafu funkce $f(x)$ s osou $x$ získáme řešením rovnice $f(x)=0$.
• intervaly spojitosti funkce
• body nespojitosti a limity v bodech nespojitosti
• určíme první derivaci funkce, kterou využijeme k určení
  • intervalů monotonie
  • stacionárních bodů a lokálních extrémů
• vypočteme druhou derivaci a s její pomocí určíme
  • intervaly konvexnosti a konkávnosti
  • inflexní body
• rovnice asymptot
• funkční hodnoty ve vybraných význačných bodech (tím jsou myšleny nejen extrémy či inflexní body, ale také body, které nám mohou poskytnout nějakou informaci o průběhu funkce mezi nimi)

Na základě získaných výsledků vyšetřování průběhu funkce pak lze sestrojit graf.

Příklad

Vyšetřujme průběh funkce $y=x\ln x$.

Zatímco $x$ je definováno pro všechna reálná čísla, logaritmus je definován pouze pro $x>0$. Definičním oborem vyšetřované funkce tedy bude $(0,+\mathrm{\infty })$.

Vzhledem k tomu, že funkce je definována pouze pro $x>0$, není periodická, ani lichá nebo sudá.

Limitu v bodě 0 určíme pomocí l'Hospitalova pravidla

$\underset{x\to 0+}{\lim }x\ln x=\underset{x\to 0+}{\lim }\frac{\ln x}{\frac{1}{x}}=\underset{x\to 0+}{\lim }\frac{\frac{1}{x}}{-\frac{1}{x^2}}=0$

Funkci lze tedy definovat také v bodě $y(0)=0$, tzn. rozšířit definiční obor na $⟨0,+\mathrm{\infty })$.

Průsečík s osou $y$ získáme dosazením $x=0$, tedy $y=0$.

Průsečík s osou $x$ získáme z rovnice $x\ln x=0$, která má řešení $x_1=0,x_2=1$.

První a druhá derivace funkce jsou

$y^{\prime }=\ln x+1$

$y^{\prime \prime }=\frac{1}{x}$

Funkce je rostoucí v intervalu, ve kterém platí $y^{\prime }>0$, což lze po dosazení zapsat jako $\ln x>-1$. Řešením získáme, že funkce je rostoucí pro $x>\frac{1}{e}$.

Funkce je klesající v intervalu, ve kterém platí $y^{\prime }<0$, tzn. $\ln x<-1$. Řešením získáme, že funkce je klesající pro $x<\frac{1}{e}$.

V bodě $x_3=\frac{1}{e}$ je $y^{\prime }(x_3)=0$. Tento bod je tedy stacionárním bodem. Již z rozložení intervalů monotonie lze určit, že se jedná o ostré lokální minimum, což lze ověřit dosazením do druhé derivace, neboť $y^{\prime \prime }(\frac{1}{e})=e>0$. Hodnota funkce v tomto bodě je $y(\frac{1}{e})=-\frac{1}{e}$.

Vzhledem k tomu, že $y^{\prime \prime }>0$ na celém definičním oboru funkce, je funkce konvexní ve všech bodech, kde je definována. Funkce nemá žádný inflexní bod.

Asymptoty k funkci neexistují, neboť $k=\underset{x\to +\mathrm{\infty }}{\lim }\frac{f(x)}{x}=\underset{x\to +\mathrm{\infty }}{\lim }\ln x=+\mathrm{\infty }$.

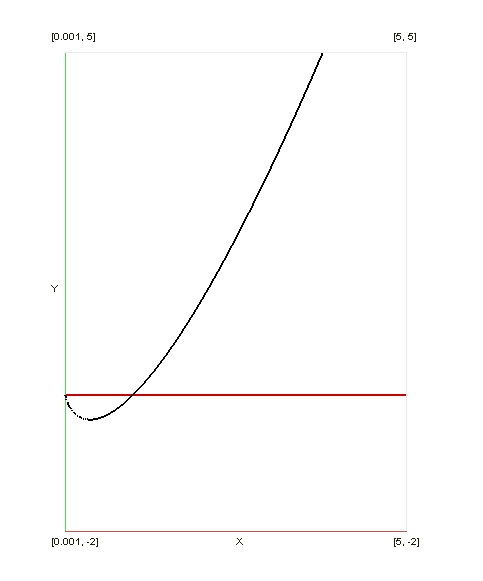
Graf vyšetřované funkce tedy bude mít následující průběh.

Příklad vyšetřování průběhu funkce.

Odkazy

Související články

• Stacionární bod
• Extrém funkce
• Konvexnost a konkávnost funkce
• Monotónní funkce

Externí odkazy

• Vykreslování grafů funkcí (i jejich derivací a integrálů)