Rovnoběžník

Rovnoběžník (Šablona:Vjazyce parallelogrammum, někdy též r(h)omboid; ve starší české literatuře kosodélník) je čtyřúhelník, jehož protilehlé strany jsou rovnoběžné.

Vlastnosti

Protější strany rovnoběžníku jsou shodné (mají stejnou délku) : $a = | A B | = | C D | = c, d = | A D | = | B C | = b .$

Protější úhly rovnoběžníku jsou shodné. Součet velikostí vnitřních úhlů čtyřúhelníku je 360°, součet dvou sousedních úhlů je 180°.

Velikost protilehlých úhlů má stejnou velikost, platí $α = ∠ D A B = ∠ B C D = γ, β = ∠ A B C = ∠ C D A = δ .$ Průsečík úhlopříček e, f rovnoběžníku je jeho středem souměrnosti. Úhlopříčka rozděluje rovnoběžník na dva shodné trojúhelníky.

Úhlopříčky rovnoběžníku se vzájemně půlí. Délky úhlopříček se počítají podle vzorce:

e = | A C | = \sqrt{a^{2} + b^{2} + 2 a b \cos α} = \sqrt{(a + h_{a} cotg α)^{2} + h_{a}^{2}},

f = | B D | = \sqrt{a^{2} + b^{2} - 2 a b \cos α} = \sqrt{(a - h_{a} cotg α)^{2} + h_{a}^{2}} .

Platí tedy rovnoběžníková rovnost:

e^{2} + f^{2} = 2 (a^{2} + b^{2})

Rovnoběžník je středově souměrný, středem souměrnosti je průsečík jeho úhlopříček.

Shrnutí vlastností čtyřúhelníků. ^[1]


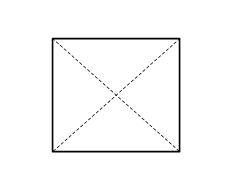
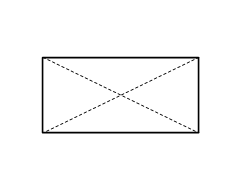
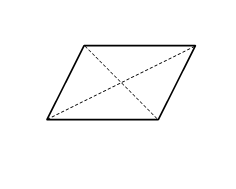
čtverec	obdélník	kosočtverec	kosodélník

všechny strany jsou stejně dlouhé	sousední strany mají různé délky	všechny strany jsou stejně dlouhé	sousední strany mají různé délky
všechny vnitřní úhly jsou pravé		žádný vnitřní úhel není pravý
úhlopříčky se navzájem půlí
úhlopříčky mají stejnou délku		úhlopříčky mají různé délky
úhlopříčky jsou k sobě kolmé	úhlopříčky nejsou k sobě kolmé	úhlopříčky jsou k sobě kolmé	úhlopříčky nejsou k sobě kolmé
úhlopříčky půlí vnitřní úhly	úhlopříčky nepůlí vnitřní úhly	úhlopříčky půlí vnitřní úhly	úhlopříčky nepůlí vnitřní úhly

Obsah

Obsah rovnoběžníku je roven: $S = a h_{a} = b h_{b} = a b \sin α$ ,

kde $a = | A B |$ a $b = | A D |$ jsou délky přilehlých stran rovnoběžníku a $h_{a}$ je výška ke straně $A B$ , obdobně $h_{b}$ je výška ke straně $A D$ , $α$ je vnitřní úhel mezi přilehlými stranami.

V rovině

Pokud jsou vrcholy $A, B, C, D$ zadány pomocí souřadnic v rovině, tj. $A = (x_{A}, y_{A})$ , $B = (x_{B}, y_{B})$ , atd., je obsah rovnoběžníku roven absolutní hodnotě determinantu sestaveného ze souřadnic libovolných tří vrcholů takto

S = | \det (\begin{matrix} x_{B} - x_{A} & x_{D} - x_{A} \\ y_{B} - y_{A} & y_{D} - y_{A} \end{matrix}) | = | (x_{B} y_{D} - x_{D} y_{B}) - (x_{A} y_{D} - x_{D} y_{A}) + (x_{A} y_{B} - x_{B} y_{A}) | .

Ztotožníme-li, pro jednoduchost, vrchol $A$ s počátkem souřadného systému, tj. $A = (0, 0)$ , pak tedy

S = | x_{B} y_{D} - x_{D} y_{B} | .

Zcela analogicky lze spočítat objem libovolného rovnoběžnostěnu, resp. nadobjem libovoného $n$ -rozměrného nadrovnoběžnostěnu (v $n$ -rozměrném prostoru).

V trojrozměrném prostoru

Pokud jsou vrcholy $A, B, C, D$ zadány pomocí souřadnic v prostoru, tj. $A = (x_{A}, y_{A}, z_{A})$ , $B = (x_{B}, y_{B}, z_{B})$ , atd., a zavedeme-li stranové vektory

𝐚 = (x_{B} - x_{A}, y_{B} - y_{A}, z_{B} - z_{A}), 𝐛 = (x_{D} - x_{A}, y_{D} - y_{A}, z_{D} - z_{A}),

je obsah rovnoběžníku roven euklidovské normě (délce) vektoru $𝐚 \times 𝐛$ , kde " $\times$ " značí vektorový součin dvou vektorů. Tedy

S = ‖ 𝐚 \times 𝐛 ‖_{2} = ((𝐚 \times 𝐛) \cdot (𝐚 \times 𝐛))^{1 / 2}

kde " $\cdot$ " značí skalární součin dvou vektorů.

Pokud mají směrové vektory nulové složky ve směru osy $z$ , tj.

𝐚 = (x_{B} - x_{A}, y_{B} - y_{A}, 0), 𝐛 = (x_{D} - x_{A}, y_{D} - y_{A}, 0),

pak

𝐚 \times 𝐛 = (0, 0, (x_{B} y_{D} - x_{D} y_{B}) - (x_{A} y_{D} - x_{D} y_{A}) + (x_{A} y_{B} - x_{B} y_{A})),

čímž dostaneme právě vztah pro výpočet obsahu rovnoběžníka v rovině.

Ztotožníme-li, pro jednoduchost, vrchol $A$ s počátkem souřadného systému, tj. $A = (0, 0, 0)$ , pak

𝐚 \times 𝐛 = (y_{B} z_{D} - y_{D} z_{B}, x_{D} z_{B} - x_{B} z_{D}, x_{B} y_{D} - x_{D} y_{B})

v obecném případě, respektive

𝐚 \times 𝐛 = (0, 0, x_{B} y_{D} - x_{D} y_{B})

v případě, že směrové vektory mají navíc nulové složky ve směru osy $z$ .

Zobecněním vektorového součinu do $n$ -rozměrného prostoru (jedná se o součin $(n - 1)$ lineárně nezávislých vektorů délky $n$ , jehož výsledkem je vektor kolmý na všechny předchozí, tvořící s nimi, v daném pořadí, pravotočivou bázi) lze zcela analogicky spočítat nadobsah libovolného $(n - 1)$ -rozměrného nadrovnoběžníku v $n$ -rozměrném prostoru.

V n-rozměrném (reálném) prostoru

Pokud je rovnoběžník dán dvěma stranovými vektory v obecném reálném $n$ -rozměrném prostoru

𝐚 = (a_{1}, a_{2}, a_{3}, \dots, a_{n}), 𝐛 = (b_{1}, b_{2}, b_{3}, \dots, b_{n}),

pak jeho obsah je dán vztahem

S = \sqrt{‖ 𝐚 ‖_{2}^{2} ‖ 𝐛 ‖_{2}^{2} - ⟨ 𝐚, 𝐛 ⟩^{2}} = ((𝐚 \cdot 𝐚) (𝐛 \cdot 𝐛) - (𝐚 \cdot 𝐛)^{2})^{1 / 2},

kde " $⟨, ⟩$ ", resp. " $\cdot$ " značí skalární součin dvou vektorů.

Dosazením

𝐚 = (x_{B} - x_{A}, y_{B} - y_{A}, 0, \dots, 0), 𝐛 = (x_{D} - x_{A}, y_{D} - y_{A}, 0, \dots, 0),

opět dostáváme známý vztah pro obsah rovnoběžníku v rovině.

Reference

↑ Šablona:Citace monografie

Literatura

Karel Rektorys a kolektiv: Přehled užité matematiky I, Prometheus, Praha 1995, Šablona:ISBN, str. 97
Marcela Palková a kolektiv: Průvodce matematikou 2, Didaktis, Brno 2007, Šablona:ISBN, str. 54-55

Související články

Externí odkazy

Šablona:Commonscat

Šablona:Pahýl Šablona:Autoritní data

Šablona:Portály

[1] Šablona:Citace monografie

[1]