Soubor:Entanglement vs classical correlation abstract picture.gif
Z testwiki
Skočit na navigaci
Skočit na vyhledávání
Entanglement_vs_classical_correlation_abstract_picture.gif (562 × 341 pixelů, velikost souboru: 1,49 MB, MIME typ: image/gif, ve smyčce, 150 snímků, 30 s)
Poznámka: Kvůli technickým omezením nebudou náhledy obrázků GIF ve vysokém rozlišení, jako je tento, animované.
Tento soubor pochází z Wikimedia Commons a mohou ho používat ostatní projekty. Níže jsou zobrazeny informace, které obsahuje jeho tamější stránka s popisem souboru.
Popis
| PopisEntanglement vs classical correlation abstract picture.gif |
English: The comparison of the quantum and classical correlations. The ring on the left corresponds to the singlet state  of polarization of two photons, which exhibits perfect correlations in any linearly polarized measurement basis. Either the magenta detectors simultaneously fire, or both orange detectors fire. The ring on the right corresponds to the dephased singlet state of polarization of two photons, which exhibits perfect correlations in any linearly polarized measurement basis. Either the magenta detectors simultaneously fire, or both orange detectors fire. The ring on the right corresponds to the dephased singlet state  , which displays only classical correlations that are perfect in the H/V basis but vanishing in the D/A basis. The latter is manifested by events when one photon activates the magenta detector whereas the other photon activates the orange detector. , which displays only classical correlations that are perfect in the H/V basis but vanishing in the D/A basis. The latter is manifested by events when one photon activates the magenta detector whereas the other photon activates the orange detector.Čeština: Porovnání kvantového provázání a klasické korelace. Kotouč nalevo odpovídá singletovému stavu  polarizace dvou fotonů, jenž vykazuje dokonalé korelace ve všech lineárně polarizovaných měřicích bázích. Buď se aktivují oba fialové detektory, nebo oba oranžové detektory. Kotouč napravo odpovídá defázovanému singletovému stavu polarizace dvou fotonů, jenž vykazuje dokonalé korelace ve všech lineárně polarizovaných měřicích bázích. Buď se aktivují oba fialové detektory, nebo oba oranžové detektory. Kotouč napravo odpovídá defázovanému singletovému stavu  , který vykazuje pouze klasické korelace, jež jsou dokonalé v bázi H/V, ale vytrácejí se v bázi D/A. Absence korelací v této bázi se projevuje tak, že v některých případech jeden foton aktivuje fialový detektor, zatímco foton druhý aktivuje oranžový detektor. , který vykazuje pouze klasické korelace, jež jsou dokonalé v bázi H/V, ale vytrácejí se v bázi D/A. Absence korelací v této bázi se projevuje tak, že v některých případech jeden foton aktivuje fialový detektor, zatímco foton druhý aktivuje oranžový detektor. |
| Datum | |
| Zdroj | Vlastní dílo |
| Autor | JozumBjada |
Licence
Já, držitel autorských práv k tomuto dílu, ho tímto zveřejňuji za podmínek následující licence:
Tento soubor podléhá licenci Creative Commons Uveďte autora-Zachovejte licenci 4.0 International
- Dílo smíte:
- šířit – kopírovat, distribuovat a sdělovat veřejnosti
- upravovat – pozměňovat, doplňovat, využívat celé nebo částečně v jiných dílech
- Za těchto podmínek:
- uveďte autora – Máte povinnost uvést autorství, poskytnout odkaz na licenci a uvést, pokud jste provedli změny. Toho můžete docílit jakýmkoli rozumným způsobem, avšak ne způsobem naznačujícím, že by poskytovatel licence schvaloval nebo podporoval vás nebo vaše užití díla.
- zachovejte licenci – Pokud tento materiál jakkoliv upravíte, přepracujete nebo použijete ve svém díle, musíte své příspěvky šířit pod stejnou nebo slučitelnou licencí jako originál.
Source code
This animation was created using Wolfram language 12.0.0 for Microsoft Windows (64-bit) (April 6, 2019). Source code follows.
(* ::Package:: *)
(* ::Title:: *)
(*Rotating disks*)
(* ::Code:: *)
(*"Created in Wolfram language - version: 12.0.0 for Microsoft Windows (64-bit) (April 6, 2019)"*)
(* ::Chapter:: *)
(*Photon sequences*)
(* ::Input::Initialization:: *)
ClearAll[probsEnt]
(*probability of detection of an entangled photon pair in one of four \
outputs, when detectors are rotated through angle \[Theta]*)
probsEnt[\[Theta]_] := {0.5, 0, 0, 0.5}
(* ::Input::Initialization:: *)
ClearAll[probsSep]
(*probability of detection of a separable photon pair in one of four \
outputs, when detectors are rotated through angle \[Theta]*)
probsSep[\[Theta]_] := {1/8. (3 + Cos[4 \[Theta]]),Cos[\[Theta]]^2 Sin[\[Theta]]^2, Cos[\[Theta]]^2 Sin[\[Theta]]^2,1/8. (3 + Cos[4 \[Theta]])}
(* ::Input::Initialization:: *)
ClearAll[generateSinglePhotonSequence]
(*generate a train of photons according to probabilities probs*)
generateSinglePhotonSequence[probs_, numOfPairs_] :=
Module[{samples,seqPh},
\[NonBreakingSpace]\[NonBreakingSpace]samples= Prepend[RandomChoice[probs->{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}},numOfPairs], {0, 0, 0, 0}];
seqPh=Rest[samples]/.{{0,0,0,1}->{True,True},{0,0,1,0}->{True,False},{0,1,0,0}->{False,True},{1,0,0,0}->{False,False}};
AppendTo[seqPh, {False, False}]
]
(* ::Chapter:: *)
(*Images*)
(* ::Input:: *)
(*(*figures in the animation are made in Blender; here simple substitutes are generated in Mathematica*)*)
(* ::Input::Initialization:: *)
{radius,width}={.9,.6};
rect=Rectangle[{-.1,radius-width},{.1,radius}];
(* ::Input::Initialization:: *)
{grayCol,redCol,greenCol}={GrayLevel[.7],Purple(*Red*),Orange(*Green*)};
brownCol=Blend[{redCol,greenCol},.5];
(* ::Input::Initialization:: *)
thickness=Thickness[.1];
connRR=Graphics[{Lighter[redCol],thickness,Line[{{0,-1},{0,1}}]}];
connRG=Graphics[{brownCol,thickness,Circle[.7{-1,1},.7,{3\[Pi]/2.,2.\[Pi]}]},PlotRange->1];
connGR=Graphics[{brownCol,thickness,Circle[.7{1,-1},.7,{\[Pi]/2.,\[Pi]}]},PlotRange->1];
connGG=Graphics[{Lighter[greenCol],thickness,Line[{{-1,0},{1,0}}]}];
(* ::Input::Initialization:: *)
ClearAll[imgDisk]
imgDisk[col1_:grayCol,col2_:grayCol,col3_:grayCol,col4_:grayCol,conn_:Graphics@{}]:=Module[{gr},
gr=Graphics[{
{Inset[conn,Center,Center,1]},
{GrayLevel[.55],
Annulus[{0,0},{radius-.6width,radius},{0,\[Pi]/2.}],
Annulus[{0,0},{radius-.6width,radius},{\[Pi],3.\[Pi]/2}]
},
{col1,Rotate[rect,0\[Pi]/2,{0,0}]},
{col2,Rotate[rect,1\[Pi]/2,{0,0}]},
{col3,Rotate[rect,2\[Pi]/2,{0,0}]},
{col4,Rotate[rect,3\[Pi]/2,{0,0}]}
},PlotRange->1];
Rasterize[gr,Background->None,ImageResolution->50]
]
(* ::Input::Initialization:: *)
(*images themselves stored in variable imgs*)
imgEmpty=imgDisk[];
imgs[False,False]=imgDisk[redCol,grayCol,redCol,grayCol,connRR];
imgs[False,True]=imgDisk[redCol,greenCol,grayCol,grayCol,connRG];
imgs[True,False]=imgDisk[grayCol,grayCol,redCol,greenCol,connGR];
imgs[True,True]=imgDisk[grayCol,greenCol,grayCol,greenCol,connGG];
(* ::Input:: *)
(*(*Append[BooleanTable[imgs[i,j],{i,j}],imgEmpty]*)*)
(* ::Chapter:: *)
(*Scene*)
(* ::Input::Initialization:: *)
ClearAll[imgFun]
imgFun[ang_,flash_,cols_]:=Module[{img},
img=If[flash,imgs@@cols,imgEmpty];
Graphics[Inset[img,Center,Center,2,AngleVector@ang],PlotRange->1,ImageSize->400]
]
(* ::Input:: *)
(*(*Manipulate[imgFun[ang,flash,{col1,col2}],{ang,0,2\[Pi]},{flash,{True,False}},{col1,{True,False}},{col2,{True,False}},Deployed->True]*)*)
(* ::Chapter:: *)
(*Animation*)
(* ::Input::Initialization:: *)
ClearAll[generateAnimation]
generateAnimation[numShots_:4]:=Module[{seqsEnt,seqsSep,animationFun,shotDuration=1./numShots,fireRat=.7,
numPhotonsPerShot=15,fontFamily="Adobe Devanagari",lab1,lab2,labelCol=GrayLevel[0.29],angleFun},
seqsEnt = generateSinglePhotonSequence[probsEnt[#], numPhotonsPerShot] & /@ Most@Subdivide[0.,(*2.*)\[Pi],numShots];
seqsSep = generateSinglePhotonSequence[probsSep[#], numPhotonsPerShot] & /@ Most@Subdivide[0.,(*2.*)\[Pi],numShots];
lab1=Text[Style[Ket["\[Psi]"],Bold,labelCol,50,FontFamily->fontFamily]];
lab2=Text[Style["\[Rho]",Bold,labelCol,60,FontFamily->fontFamily]];
animationFun[ratIn_]:=Module[{rat=ratIn,ang,flash,idx,idx2=1,rat2,len},
rat=Clip[rat,{0,1.-1*^-6}];
{rat,idx}={numShots Mod[rat, 1/numShots], Floor[rat numShots] + 1};
ang=(*2*)\[Pi] shotDuration (idx-1);
flash=(rat<fireRat);
If[flash,
idx2= Floor[rat numPhotonsPerShot/fireRat] + 1;
,
ang+=(*2*)\[Pi] shotDuration Rescale[rat,{fireRat,1.},{0.,1}];
];
Grid[{{imgFun[ang,flash,seqsEnt[[idx,idx2]]],imgFun[ang,flash,seqsSep[[idx,idx2]]]},{lab1,lab2}}]
];
animationFun
]
(* ::Chapter:: *)
(*Rasterization*)
(* ::Input::Initialization:: *)
ClearAll[rasterizeFrameSequence]
rasterizeFrameSequence[fun_, numOfFrames_ : 10, imgResolution_ : 70] :=
Module[{time, frames},
{time, frames} = AbsoluteTiming[
Map[
Rasterize[fun[#], Background->None,ImageResolution->imgResolution]&,
Subdivide[0, 1., numOfFrames - 1]
]
];
Print["execution time: ",DateString[time, {"Minute", " m ", "Second", " s"}]];
Print["size: ", ByteCount[frames]/1024/1024., " MB"];
frames
]
(* ::Chapter:: *)
(*Export*)
(* ::Input::Initialization:: *)
filename = "test2.gif";
anim = generateAnimation[4];
(* ::Input::Initialization:: *)
frames =rasterizeFrameSequence[anim,30,50];
(* ::Input:: *)
(*(*ListAnimate[frames, AnimationRate -> 3.]*)*)
(* ::Input::Initialization:: *)
SetDirectory[NotebookDirectory[]]
Export[filename,frames,
"DisplayDurations" -> 0.2,
"ColorMapLength" -> 256/2,
AnimationRepetitions -> Infinity,
Dithering -> None]
Popisky
Přidejte jednořádkové vysvětlení, co tento soubor představuje
Abstract comparison of entanglement and classical correlations.
Položky vyobrazené v tomto souboru
zobrazuje
Nějaká hodnota bez položky na Wikidatech
9. 12. 2020
Historie souboru
Kliknutím na datum a čas se zobrazí tehdejší verze souboru.
| Datum a čas | Náhled | Rozměry | Uživatel | Komentář | |
|---|---|---|---|---|---|
| současná | 9. 12. 2020, 20:21 | 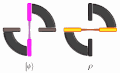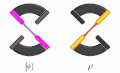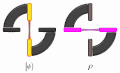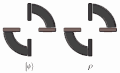 | 562 × 341 (1,49 MB) | wikimediacommons>JozumBjada | Cross-wiki upload from cs.wikipedia.org |
Využití souboru
Tento soubor používá následující stránka:
